Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T14:08:16.399Z Has data issue: false hasContentIssue false
  • English
  • Français

Limiting crossing probabilities of random fields

Part of: Stochastic processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

L. Pereira  and
H. Ferreira
L. Pereira*
Affiliation:
University of Beira Interior
H. Ferreira*
Affiliation:
University of Beira Interior
*
∗Postal address: Department of Mathematics, University of Beira Interior, 6200 Covilhã, Portugal.
∗∗Email address: helena@mat.ubi.pt
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Random fields on 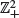, with long-range weak dependence for each coordinate individually, usually present clustering of high values. For each one of the eight directions in 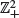, we formulate restriction conditions on local occurrence of two or more crossings of high levels. These smooth oscillation conditions enable computation of the extremal index as a clustering measure from the limiting mean number of crossings. In fact, only four directions must be inspected since for opposite directions we find the same local path crossing behaviour and the same limiting mean number of crossings. The general theory is illustrated with several 1-dependent nonstationary random fields.

Keywords

Random fielddependencenonstationarityextremal index

MSC classification

Primary: 60G60: Random fields 60G70: Extreme value theory; extremal processes 60F99: None of the above, but in this section
Type
Research Article
Information
Journal of Applied Probability , Volume 43 , Issue 3 , September 2006 , pp. 884 - 891
Copyright
© Applied Probability Trust 2006 

References

Adler, R. J. (1981). The Geometry of Random Fields. John Wiley, New York.Google Scholar
Choi, H. (2002). Central limit theory and extremes of random fields. , University of North Carolina at Chapel Hill.Google Scholar
Ferreira, H. (1994). Condições de dependência local em teoria de valores extremos. , University of Coimbra.Google Scholar
Ferreira, H. and Pereira, L. (2005). How to compute the extremal index of stationary random fields. Preprint 10/2005, University of Lisbon.Google Scholar
Hüsler, J. (1986). Extreme values of non-stationary random sequences. J. Appl. Prob. 23, 937–950.CrossRefGoogle Scholar
Hüsler, J. (1993). A note on exceedances and rare events of non-stationary sequences. J. Appl. Prob. 30, 877–888.CrossRefGoogle Scholar
Leadbetter, M. R. (1983). Extremes and local dependence in stationary sequences. Z. Wahrscheinlichkeitsth. 65, 291–306.CrossRefGoogle Scholar
Leadbetter, M. R. and Nandagopalan, S. (1989). On exceedance point processes for stationary sequences under mild oscillation restrictions. In Extreme Value Theory (Lecture Notes Statist. 51), eds Hüsler, J. and Reiss, R.-D., Springer, New York, pp. 69–80.Google Scholar
Leadbetter, M. R. and Rootzén, H. (1998). On extreme values in stationary random fields. In Stochastic Processes and Related Topics, Birkhäuser, Boston, MA, pp. 275–285.CrossRefGoogle Scholar
Leadbetter, M. R., Lindgren, G. and Rootzén, H. (1983). Extremes and Related Properties of Random Sequences and Processes. Springer, New York.Google Scholar
Pereira, L. and Ferreira, H. (2005). Extremes of quasi-independent random fields and clustering of high values. WSEAS Trans. Math. 4, 333–338.Google Scholar
Pereira, L. and Ferreira, H. (2005). On extreme values in non stationary random fields. Preprint 9/2005, University of Lisbon.Google Scholar
Piterbarg, V. I. (1996). Asymptotic Methods in the Theory of Gaussian Processes and Fields (Trans. Math. Monogr. 148). American Mathematical Society, Providence, RI.Google Scholar