Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T06:48:48.555Z Has data issue: false hasContentIssue false
  • English
  • Français

L'intégrale du mouvement brownien

Part of: Markov processes Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Aimé Lachal
Aimé Lachal*
Affiliation:
Université Claude Bernard–Lyon I
*
∗ Postal address: Laboratoire d'Analyse Fonctionelle et Probabilités, Institut de Mathématiques et Informatique, Université Claude Bernard–Lyon I, 43, Boulevard du 11 Novembre 1918, 69622 Villeurbanne Cedex, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

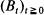Let be the Brownian motion process starting at the origin, 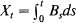its primitive and Ut = (Xt+x + ty, Bt + y), 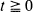, the associated bidimensional process starting from a point 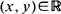. In this paper we present an elementary procedure for re-deriving the formula of Lefebvre (1989) giving the Laplace–Fourier transform of the distribution of the couple (σ α, Uσa), as well as Lachal's (1991) formulae giving the explicit Laplace–Fourier transform of the law of the couple (σ ab, Uσab), where σ α and σ ab denote respectively the first hitting time of 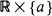from the right and the first hitting time of the double-sided barrier 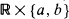by the process 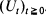. This method, which unifies and considerably simplifies the proofs of these results, is in fact a ‘vectorial' extension of the classical technique of Darling and Siegert (1953). It rests on an essential observation (Lachal (1992)) of the Markovian character of the bidimensional process .

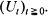Using the same procedure, we subsequently determine the Laplace–Fourier transform of the conjoint law of the quadruplet (σ α, Uσa, σb, Uσb).

Keywords

FIRST HITTING TIMESBIDIMENSIONAL PROCESSESLAPLACE–FOURIER TRANSFORM

MSC classification

Primary: 60J65: Brownian motion
Secondary: 60G40: Stopping times; optimal stopping problems; gambling theory 60G17: Sample path properties 60G15: Gaussian processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 1 , March 1993 , pp. 17 - 27
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

[1] Abramowitz, M. and Stegun, L. A. (1972) Handbook of Mathematical Functions with Formulas, and Mathematical Tables. Wiley, New York.Google Scholar
[2] Darling, D. A. and Siegert, A. J. F. (1953) The first passage problem for a continuous Markov process. Ann. Math. Statist. 24, 624–639.CrossRefGoogle Scholar
[3] Kac, M. (1962) Probability theory: its role and its impact. SIAM Rev. 4, pp. 1–11.Google Scholar
[4] Lachal, A. (1990) Sur l'intégrale du mouvement brownien. C. R. Acad. Sci. Paris 311, série I, 461–464.Google Scholar
[5] Lachal, A. (1991) Sur le premier instant de passage de l'intégrale du mouvement brownien. Ann. Inst. H. Poincaré. B27, 385–405.Google Scholar
[6] Lachal, A. (1992) Etude des trajectoires de la primitive du mouvement brownien. Thèse de Doctorat.Google Scholar
[7] Lefebvre, M. (1989) First passage densities for a two-dimensional process. SIAM J. Appl. Math. 49, 1514–1523.Google Scholar
[8] Lefebvre, M. and Whittle, P. (1988) Survival optimization for a dynamic system. Ann. Sc. Math. Québec, 12, 101–119.Google Scholar
[9] Mc Kean, H. P. Jr. (1963) A winding problem for a resonator driven by a white noise. J. Math. Kyoto Univ. 2, 227–235.Google Scholar
[10] Rice, S. O. (1944) (1945) Mathematical analysis of random noise. Bell System Tech. J. 23, 282–332; 24, 46-156.Google Scholar