Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T13:23:02.513Z Has data issue: false hasContentIssue false
  • English
  • Français

The Martin boundary for Polya's urn scheme, and an application to stochastic population growth

Published online by Cambridge University Press:  14 July 2016

David Blackwell  and
David Kendall
David Blackwell
Affiliation:
University of California
David Kendall
Affiliation:
University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

1. In 1923 Eggenberger and Pólya introduced the following ‘urn scheme’ as a model for the development of a contagious phenomenon. A box contains b black and r red balls, and a ball is drawn from it at random with ‘double replacement’ (i.e. whatever ball is drawn, it is returned to the box together with a fresh ball of the same colour); the procedure is then continued indefinitely. A slightly more complicated version with m-fold replacement is sometimes discussed, but it will be sufficient for our purposes to keep m = 2 and it will be convenient further to simplify the scheme by taking b = r = 1 as the initial condition. We shall however generalise the scheme in another direction by allowing an arbitrary number k(≧2) of colours. Thus initially the box will contain k differently coloured balls and successive random drawings will be followed by double replacement as before. We write sn (a k-vector with jth component 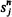) for the numerical composition of the box immediately after the nth replacement, so that 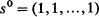and we observe that 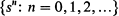is a Markov process for which the state-space consists of all ordered k-ads of positive integers, the (constant) transition-probability matrix having elements determined by 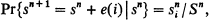where Sn is the sum of the components of sn and (e(i))j = δij. We shall calculate the Martin boundary for this Markov process, and point out some applications to stochastic models for population growth.

Type
Research Papers
Information
Journal of Applied Probability , Volume 1 , Issue 2 , December 1964 , pp. 284 - 296
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bayes, Rev. T. (1763) An essay towards solving a problem in the doctine of chances. Phil. Trans. 53, 370–418.Google Scholar
[2] Bonsall, F. F. (1963) On the representation of points of a convex set. J. Lond. Math. Soc. 38, 332–334.Google Scholar
[3] Crofton, M. W. (1885) Probability. Encyclopaedia Britannica. (9th edition) 19, 788–809.Google Scholar
[4] Doob, J. L. (1959) Discrete potential theory and boundaries. J. Math. and Mech. 8, 433–458.Google Scholar
[5] Doob, J. L., Snell, J. L. and Williamson, R. E. (1960) Application of boundary theory to sums of independent random variables. In Contributions to Probability and Statistics. Ed. Olkin, I. et al. Stanford.Google Scholar
[6] Eggenberger, F. and Pólya, G. (1923) Uber die Statistik verketteter Vorgänge. Zeit. angew. Math. Mech. 3, 279–289.CrossRefGoogle Scholar
[7] Feller, W. (1957) An Introduction to Probability Theory and its Applications I. (2nd ed.) John Wiley, New York.Google Scholar
[8] Hunt, G. A. (1960) Markoff chains and Martin boundaries. Illinois J. Math. 4, 313–340.Google Scholar
[9] Kendall, D. G. (1949) Stochastic processes and population growth. J. R. Statist. Soc. B 11, 230–264.Google Scholar
[10] Lamperti, J. and Snell, J. L. (1963) Martin boundaries for certain Markov chains. J. Math. Soc. Japan 15, 113–128.Google Scholar
[11] Lorentz, G. G. (1953) Bernstein Polynomials. Toronto.Google Scholar
[12] Watanabe, T. (1960) On the theory of Martin boundaries induced by countable Markov processes. Mem. Coll. Sci. Kyoto A 33, 39–108.Google Scholar
[13] Watanabe, T. (1960) A probabilistic method in Hausdorff moment problem and Laplace-Stieltjes transform. J. Math. Soc. Japan 12, 192–206.Google Scholar
[14] Watanabe, T. (1961) Some topics related to Martin boundaries induced by countable Markov processes. Bull, I. S. I. 38, 625–633.Google Scholar
[15] Whittaker, E. T. and Watson, G. N. (1927) A Course of Modern Analysis (4th ed.) Cambridge.Google Scholar