Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T10:25:57.435Z Has data issue: false hasContentIssue false
  • English
  • Français

A model for a system subject to random shocks

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

Eui Yong Lee  and
Jiyeon Lee
Eui Yong Lee
Affiliation:
Pohang Institute of Science and Technology
Jiyeon Lee*
Affiliation:
Pohang Institute of Science and Technology
*
∗ Postal address: Department of Mathematics, Pohang Institute of Science and Technology, P.O. Box 125, Pohang 790–600, Korea.
Get access Rights & Permissions [Opens in a new window]

Abstract

A Markovian stochastic model for a system subject to random shocks is introduced. It is assumed that the shock arriving according to a Poisson process decreases the state of the system by a random amount. It is further assumed that the system is repaired by a repairman arriving according to another Poisson process if the state when he arrives is below a threshold α. Explicit expressions are deduced for the characteristic function of the distribution function of X(t), the state of the system at time t, and for the distribution function of X(t), if 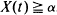. The stationary case is also discussed.

Keywords

POISSON PROCESSREPAIRMANTHRESHOLDINTEGRO-DIFFERENTIAL EQUATIONCHARACTERISTIC FUNCTIONRENEWAL PROCESSSTATIONARY DISTRIBUTION

MSC classification

Primary: 60K10: Applications (reliability, demand theory, etc.)
Type
Short Communications
Information
Journal of Applied Probability , Volume 30 , Issue 4 , December 1993 , pp. 979 - 984
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research has been supported by the Korea Science and Engineering Foundation (KOSEF), under Grant Number 913-0105-002-2.

References

[1] Baxter, L. A. and Lee, E. Y. (1987) An inventory with constant demand and Poisson restocking. Prob. Eng. Inf. Sci. 1, 203–210.Google Scholar
[2] Baxter, L. A. and Lee, E. Y. (1987) A diffusion model for a system subject to continuous wear. Prob. Eng. Inf. Sci. 1, 405–416.Google Scholar
[3] Feller, W. (1936) Zur Theorie der Stochastischen Prozesse (Existenz und Eindeutigkeitssätze). Math. Ann. 113, 13–60.Google Scholar
[4] Silver, E. A. and Peterson, R. (1985) Decision Systems for Inventory Management and Production Planning, 2nd edn. Wiley, New York.Google Scholar