Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T22:10:17.535Z Has data issue: false hasContentIssue false
  • English
  • Français

Modeling the effect of erosion on crop production

Published online by Cambridge University Press:  14 July 2016

P. Todorovic  and
J. Gani
P. Todorovic*
Affiliation:
University of Kentucky
J. Gani*
Affiliation:
University of California, Santa Barbara
*
∗Postal address for both authors: Statistics Program, Department of Mathematics, University of California, Santa Barbara, CA 93106, USA.
∗Postal address for both authors: Statistics Program, Department of Mathematics, University of California, Santa Barbara, CA 93106, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with a model for the effect of erosion on crop production. Crop yield in the year n is given by X(n) = YnLn, where 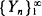is a sequence of strictly positive i.i.d. random variables such that E{Y1} <∞, and is a Markov chain with stationary transition probabilities, independent of 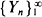. When suitably normalized, 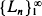leads to a martingale which converges to 0 almost everywhere (a.e.) as n → ∞. In addition, for large n, the distribution of Ln is approximately lognormal. The conditional expectations and probabilities of 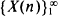, given the past history of the process, are determined. Finally, the asymptotic behaviour of the total crop yield 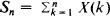is discussed. It is established that under certain regularity conditions Sn converges a.e. to a finite-valued random variable S whose Laplace transform can be obtained as the solution of a Volterra-type linear integral equation.

Keywords

PRODUCT OF RANDOM VARIABLESMARKOV CHAINMARTINGALELIMIT THEOREMSINTEGRAL EQUATION
Type
Research Papers
Information
Journal of Applied Probability , Volume 24 , Issue 4 , December 1987 , pp. 787 - 797
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported in part by the Office of Naval Research, Contract No. N00014-84-K-0568.

References

Feller, W. (1971) An Introduction to Probability Theory and Its Applications , Vol. 2, 2nd edn. Wiley, New York.Google Scholar
Kolmogorov, A. N. (1941) Über das logarithmisch normale Verteilungsgesetz der Dimensionen der Teilchen bei Zerstückelung. Dokl. Akad. Nauk SSR. 31, 99–101.Google Scholar
Lomnicki, Z. A. (1967) On the distribution of products of random variables. J.R. Statist. Soc. B 29, 513–524.Google Scholar
Springer, M. D. (1979) The Algebra of Random Variables. Wiley, New York.Google Scholar
Springer, M. D. and Thompson, W. E. (1966) The distribution of products of independent random variables. SIAM J. Appl. Math. 14, 511–526.CrossRefGoogle Scholar
Todorovic, P. (1987) Limit theorems arising in soil erosion modeling. In Applied Probability, Stochastic Processes and Sampling Theory , eds. MacNeill, Ian B. and Umphrey, Gary J. Reidel, Dordrecht, 65–73.CrossRefGoogle Scholar