Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Doney, R.A.
1982.
On the exact asymptotic behaviour of the distribution of ladder epochs.
Stochastic Processes and their Applications,
Vol. 12,
Issue. 2,
p.
203.
Doney, R. A.
1982.
On the existence of the mean ladder height for random walk.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 59,
Issue. 3,
p.
373.
Sunyach, C.
1985.
Marches aléatoires récurrentes totalement dissymétriques et domaine d⊃attraction des lois stables.
Stochastics,
Vol. 14,
Issue. 4,
p.
327.
Chow, Y.S
1986.
On moments of ladder height variables.
Advances in Applied Mathematics,
Vol. 7,
Issue. 1,
p.
46.
Grübel, Rudolf
1986.
A note on the distance of ladder height distributions.
Stochastic Processes and their Applications,
Vol. 23,
Issue. 2,
p.
339.
Janson, Svante
1986.
Moments for first-passage and last-exit times, the minimum, and related quantities for random walks with positive drift.
Advances in Applied Probability,
Vol. 18,
Issue. 4,
p.
865.
Biggins, J. D.
and
Kyprianou, A. E.
2004.
Measure change in multitype branching.
Advances in Applied Probability,
Vol. 36,
Issue. 2,
p.
544.
Caravenna, Francesco
2005.
A local limit theorem for random walks conditioned to stay positive.
Probability Theory and Related Fields,
Vol. 133,
Issue. 4,
p.
508.
Aleškevičienė, A. K.
2006.
On calculation of moments of ladder heights.
Lithuanian Mathematical Journal,
Vol. 46,
Issue. 2,
p.
129.
Сгибнев, Михаил Сергеевич
and
Sgibnev, Mikhail Sergeyevich
2007.
Об однородном консервативном уравнении Винера - Хопфа.
Математический сборник,
Vol. 198,
Issue. 9,
p.
123.
Nagaev, S. V.
2008.
Exact expressions for moments of ladder heights.
Doklady Mathematics,
Vol. 78,
Issue. 3,
p.
916.
Sgibnev, M S
2008.
Semimultiplicative moments of factors in Wiener-Hopf matrix factorization.
Sbornik: Mathematics,
Vol. 199,
Issue. 2,
p.
277.
Aleškevičienė, A.K.
2008.
On the existence of moments of ladder heights.
Statistics & Probability Letters,
Vol. 78,
Issue. 3,
p.
282.
Сгибнев, Михаил Сергеевич
and
Sgibnev, Mikhail Sergeyevich
2008.
Полумультипликативные моменты сомножителей матричной факторизации Винера - Хопфа.
Математический сборник,
Vol. 199,
Issue. 2,
p.
115.
Gut, Allan
2009.
Stopped Random Walks.
p.
49.
Nagaev, S. V.
2010.
Exact expressions for the moments of ladder heights.
Siberian Mathematical Journal,
Vol. 51,
Issue. 4,
p.
675.
Iksanov, Alexander
and
Meiners, Matthias
2010.
Exponential Moments of First Passage Times and Related Quantities for Random Walks.
Electronic Communications in Probability,
Vol. 15,
Issue. none,
Aïdékon, Elie
Hu, Yueyun
and
Zindy, Olivier
2013.
The precise tail behavior of the total progeny of a killed branching random walk.
The Annals of Probability,
Vol. 41,
Issue. 6,
Hu, Yueyun
2016.
How big is the minimum of a branching random walk?.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 52,
Issue. 1,
Burdzy, Krzysztof
and
Tadić, Tvrtko
2017.
Can one make a laser out of cardboard?.
The Annals of Applied Probability,
Vol. 27,
Issue. 4,


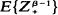 and
and 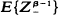 are both finite.
are both finite.