Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-14T04:05:40.879Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple buying or selling with vector offers

Part of: Sequential methods Stochastic processes

Published online by Cambridge University Press:  14 July 2016

F. Thomas Bruss  and
Thomas S. Ferguson
F. Thomas Bruss*
Affiliation:
Université Libre de Bruxelles
Thomas S. Ferguson*
Affiliation:
University of California, Los Angeles
*
∗Postal address: Université Libre de Bruxelles, Département de Mathématique et Institut de Statistique, CP 210, B-1050 Brussels, Belgium. e-mail: tbruss@ulb.ac.be
∗Postal address: Université Libre de Bruxelles, Département de Mathématique et Institut de Statistique, CP 210, B-1050 Brussels, Belgium. e-mail: tbruss@ulb.ac.be
Get access Rights & Permissions [Opens in a new window]

Abstract

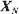We consider a generalization of the house-selling problem to selling k houses. Let the offers, X1, X2, · ··, be independent, identically distributed k-dimensional random vectors having a known distribution with finite second moments. The decision maker is to choose simultaneously k stopping rules, N1, · ··, Nk, one for each component. The payoff is the sum over j of the jth component of minus a constant cost per observation until all stopping rules have stopped. Simple descriptions of the optimal rules are found. Extension is made to problems with recall of past offers and to problems with a discount.

Keywords

OPTIMAL STOPPINGHOUSE-SELLINGJOB SEARCHCOSTDISCOUNTRECALLCONVEX SET FUNCTION

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 62L15: Optimal stopping
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 4 , December 1997 , pp. 959 - 973
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albright, S. C. (1974) Optimal sequential assignments with random arrival times. Management Sci. 21, 60–70.CrossRefGoogle Scholar
Collins, E. J. and Mcnamara, J. M. (1993) The job-search problem with competition: An evolutionarily stable dynamic strategy. Adv. Appl. Prob. 25, 314–333.Google Scholar
Chow, Y. S. and Robbins, H. (1961) A martingale system theorem and applications. Fourth Berkeley Symp. on Math. Statist. Prob. 1, 93–104.Google Scholar
Chow, Y. S., Robbins, H. and Siegmund, D. (1971) Great Expectations: The Theory of Optimal Stopping. Houghton Mifflin, Boston.Google Scholar
David, I. and Yechiali, U. (1986) Sequential assignment match processes with arrivals of candidates and offers. Prob. Eng. Inf. Sci. 4, 413–430.Google Scholar
Degroot, M. H. (1970) Optimal Statistical Decisions. McGraw-Hill, New York.Google Scholar
Delbaen, F. (1994) Private communication.Google Scholar
Derman, C., Lieberman, G. J. and Ross, S. M. (1972) A sequential stochastic assignment problem. Management Sci. 18, 349–355.Google Scholar
Derman, C. and Sacks, J. (1960) Replacement of periodically inspected equipment. Naval Res. Logist. Quart. 7, 597–607.Google Scholar
Karlin, S. (1962) Stochastic models and optimal policy for selling an asset. In Studies in Applied Probability and Management Science. Stanford University Press, Stanford, CA. pp. 148–158.Google Scholar
Macqueen, J. and Miller, R. G. (1960) Optimal persistence policies. Operat. Res. 8, 362–380.Google Scholar
Mcmillan, J. and Rothschild, M. (1994) Search. In Handbook of Game Theory with Economic Applications 2. ed. Aumann, R. J. and Hart, S. North Holland/Elsevier, New York. pp. 905–927.Google Scholar
Mcnamara, J. M. and Collins, E. J. (1990) The job-search problem as an employer-candidate game. J. Appl. Prob. 27, 815–827.Google Scholar
Nakai, T. (1986) An optimal selection problem for a sequence with a random number of applicants per period. Operat. Res. 34, 478–485.Google Scholar
Righter, R. (1990) Stochastically maximizing the number of successes in a sequential assignment problem. J. Appl. Prob. 27, 351–364.Google Scholar
Saario, V. (1986) Comparison of the discrete and continuous-time stochastic selling models. Eng. Costs Production Econ. 12, 15–20.Google Scholar
Saario, V. and Sakaguchi, M. (1990) Some generalized house-selling problems. Math. Japonica 35, 861–873.Google Scholar
Sakaguchi, M. (1961) Dynamic programming of some sequential sampling design. J. Math. Anal. Appl. 2, 446–466.Google Scholar
Sakaguchi, M. (1973) Optimal stopping in sampling from a bivariate distribution. J. Operat. Res. Soc. Japan 16, 186–200.Google Scholar
Sakaguchi, M. (1978) When to stop: randomly appearing bivariate target values. J. Operat. Res. Soc. Japan 21, 45–58.Google Scholar
Shapley, L. S. (1971) Cores of convex games. Int. J. Game Theory 1, 11–26.Google Scholar
Stadje, W. (1985) On multiple stopping rules. Optimization 16, 410–418.Google Scholar
Stadje, W. (1990) A full information pricing problem for the sale of several identical commodities. Z. Operat. Res. 34, 161–181.Google Scholar
Stigler, G. J. (1961) The economics of information. J. Political Econ. 69, 213–225.Google Scholar
Stigler, G. J. (1962) Information in the labor market. J. Political Econ. 70, 94–105.Google Scholar