Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Weissman, Ishay
1978.
Estimation of Parameters and Large Quantiles Based on thekLargest Observations.
Journal of the American Statistical Association,
Vol. 73,
Issue. 364,
p.
812.
Gomes, M. Ivette
1981.
Statistical Distributions in Scientific Work.
p.
389.
Weissman, Ishay
1981.
Confidence intervals for the threshold parameter.
Communications in Statistics - Theory and Methods,
Vol. 10,
Issue. 6,
p.
549.
Nagaraja, H. N.
1982.
Record values and extreme value distributions.
Journal of Applied Probability,
Vol. 19,
Issue. 01,
p.
233.
Davis, Richard A
1983.
Limit laws for upper and lower extremes from stationary mixing sequences.
Journal of Multivariate Analysis,
Vol. 13,
Issue. 2,
p.
273.
Gomes, M. Ivette
1984.
Penultimate limiting forms in extreme value theory.
Annals of the Institute of Statistical Mathematics,
Vol. 36,
Issue. 1,
p.
71.
Falk, M.
1986.
Rates of uniform convergence of extreme order statistics.
Annals of the Institute of Statistical Mathematics,
Vol. 38,
Issue. 2,
p.
245.
Gomes, M. Ivette
and
Pestana, Dinis D.
1986.
Insurance and Risk Theory.
p.
301.
Hsing, Tailen
1987.
On the characterization of certain point processes.
Stochastic Processes and their Applications,
Vol. 26,
Issue. ,
p.
297.
Athayde, Emilia
and
Gomes, M. Ivette
1987.
Mathematical Statistics and Probability Theory.
p.
1.
Dagsvik, John K.
1988.
Markov chains generated by maximizing components of multidimensional extremal processes.
Stochastic Processes and their Applications,
Vol. 28,
Issue. 1,
p.
31.
1988.
Extreme Value Theory in Engineering.
p.
341.
Falk, Michael
1989.
Extreme Value Theory.
Vol. 51,
Issue. ,
p.
1.
Gomes, M. Ivette
1989.
Extreme Value Theory.
Vol. 51,
Issue. ,
p.
191.
Chakravarthi, P.R.
Weiner, D.D.
and
Ozturk, A.
1991.
On determining the radar threshold from experimental data.
p.
594.
Hasofer, A. M.
and
Wang, Z.
1992.
A Test for Extreme Value Domain of Attraction.
Journal of the American Statistical Association,
Vol. 87,
Issue. 417,
p.
171.
David, H. A.
1994.
Extreme Value Theory and Applications.
p.
211.
Weissman, Ishay
1995.
The indices of the largest amongnindependent observations.
Communications in Statistics. Stochastic Models,
Vol. 11,
Issue. 4,
p.
613.
Balkema, A.A.
and
Pancheva, E.I.
1996.
Decomposition for multivariate extremal processes.
Communications in Statistics - Theory and Methods,
Vol. 25,
Issue. 4,
p.
737.
Weissman, Ishay
1997.
Fitting a Mejzler distribution to extreme value data.
Journal of Statistical Planning and Inference,
Vol. 61,
Issue. 1,
p.
39.

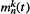 be the
be the 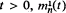 converges in distribution. Then all the finite-dimensional laws of
converges in distribution. Then all the finite-dimensional laws of  converge. The limiting process is represented in terms of a non-homogeneous two-dimensional Poisson process.
converge. The limiting process is represented in terms of a non-homogeneous two-dimensional Poisson process.