Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Isham, Valerie
and
Westcott, Mark
1979.
A self-correcting point process.
Stochastic Processes and their Applications,
Vol. 8,
Issue. 3,
p.
335.
STIRZAKER, D.
1990.
Divergent growth processes.
International Journal of Systems Science,
Vol. 21,
Issue. 4,
p.
799.
Mehta, A
and
Luck, J M
2011.
Power-law forgetting in synapses with metaplasticity.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2011,
Issue. 09,
p.
P09025.

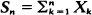 of independent random variables converges in distribution when suitably normalised, so long as the
of independent random variables converges in distribution when suitably normalised, so long as the