Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Keilson, Julian
1971.
Log-concavity and log-convexity in passage time densities of diffusion and birth-death processes.
Journal of Applied Probability,
Vol. 8,
Issue. 2,
p.
391.
Keilson, Julian
1971.
Log-concavity and log-convexity in passage time densities of diffusion and birth-death processes.
Journal of Applied Probability,
Vol. 8,
Issue. 02,
p.
391.
Steutel, F.W.
1973.
Some recent results in infinite divisibility.
Stochastic Processes and their Applications,
Vol. 1,
Issue. 2,
p.
125.
Steutel, F. W.
1973.
Some recent results in infinite divisibility.
Advances in Applied Probability,
Vol. 5,
Issue. 1,
p.
25.
Holden, A. V.
and
Ramadan, S. M.
1980.
Identification of endogenous and exogenous activity in a molluscan neurone by spike train analysis.
Biological Cybernetics,
Vol. 37,
Issue. 2,
p.
107.
Bondesson, Lennart
1981.
Classes of infinitely divisible distributions and densities.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 57,
Issue. 1,
p.
39.
Angelini, F.
Barbi, M.
Chillemi, S.
and
Petracchi, D.
1982.
Biomathematics in 1980 - Papers presented at a workshop on Biomathematics: Current Status and Future Perspectives, Salerno, April 1980.
Vol. 58,
Issue. ,
p.
87.
Holden, A. V.
1983.
Stochastic processes in neurophysiology: Transformation from point to continuous processes.
Bulletin of Mathematical Biology,
Vol. 45,
Issue. 4,
p.
443.
Kent, John T.
and
Longford, Nicholas T.
1983.
An eigenvalue decomposition for first hitting times in random walks.
Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 63,
Issue. 1,
p.
71.
Sumita, Ushio
and
Masuda, Yasushi
1987.
Classes of probability density functions having Laplace transforms with negative zeros and poles.
Advances in Applied Probability,
Vol. 19,
Issue. 3,
p.
632.
Manoharan, M.
Alamatsaz, M.H.
and
Shanbhag, D.N.
2003.
Stochastic Processes: Modelling and Simulation.
Vol. 21,
Issue. ,
p.
557.

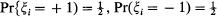 . The process
. The process 