Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Iglehart, Donald L.
and
Kennedy, Douglas P.
1970.
Weak convergence of the average of flag processes.
Journal of Applied Probability,
Vol. 7,
Issue. 3,
p.
747.
Iglehart, Donald L.
and
Kennedy, Douglas P.
1970.
Weak convergence of the average of flag processes.
Journal of Applied Probability,
Vol. 7,
Issue. 03,
p.
747.
Kovalenko, I. N.
1974.
Queueing theory.
Journal of Soviet Mathematics,
Vol. 2,
Issue. 1,
p.
1.

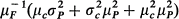 where
where 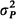 and
and 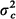 are the variances and
are the variances and 