No CrossRef data available.
Article contents
On a characterization property of finite irreducible Markov chains
Published online by Cambridge University Press: 14 July 2016
Extract
Let {Xk }, k = 1, 2, ··· be a sequence of random variables forming a homogeneous Markov chain on a finite state-space, S = {1, 2, ···, s}. Xk could be thought of as the state at time k of some physical system for which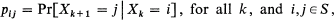 are the (one-step) transition probabilities. It is assumed that all the states are inter-communicating, so that the transition matrix P = ((pij )) is irreducible.
are the (one-step) transition probabilities. It is assumed that all the states are inter-communicating, so that the transition matrix P = ((pij )) is irreducible.
Information
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust 1970
References
Bhat, B. R. (1960) Maximum likelihood estimation for positively regular Markov chains. Sankhya
22, 339–344.Google Scholar
Gani, J. (1955) Some theorems and sufficiency conditions for the maximum likelihood estimator of an unknown parameter in a simple Markov chain. Biometrika
42, 342–359.Google Scholar
Kingman, J. F. C. (1963) Poisson counts for random sequences of events. Ann. Math. Statist.
34, 1217–1232.CrossRefGoogle Scholar

