Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1975.
Discussion of the Paper by Dr Cliff and Dr Ord.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 37,
Issue. 3,
p.
328.
Isham, Valerie
1977.
A Markov construction for a multidimensional point process.
Journal of Applied Probability,
Vol. 14,
Issue. 03,
p.
507.
Neveu, J.
1977.
Ecole d’Eté de Probabilités de Saint-Flour VI-1976.
Vol. 598,
Issue. ,
p.
249.

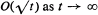 . Some generalisations are discussed.
. Some generalisations are discussed.