Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T01:03:27.648Z Has data issue: false hasContentIssue false
  • English
  • Français

On crossing times for multidimensional walks with skip-free components

Part of: Markov processes Combinatorial probability Stochastic processes

Published online by Cambridge University Press:  14 July 2016

K. A. Borovkov
K. A. Borovkov*
Affiliation:
Steklov Mathematical Institute
*
∗Postal address: Steklov Mathematical Institute, Vavilov st. 42, 117966 Moscow GSP–1, Russia.
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper deals with processes in 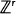(or 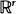), one of whose components is skip-free. We obtain identities for distributions of hitting times for the components of the process generalizing the well-known one for the one-dimensional case. These relations reflect the fact that in this case spatial and time coordinates play, in some sense, symmetric roles. They turn out to be useful for solving several problems. For example, they allow us to find the distribution of the number of jumps of the process, which fall in a fixed set before the skip-free component of the process hits a fixed level. Examples are given showing how our results can be applied to models in branching processes, queueing, and risk theory.

Keywords

SKIP-FREE RANDOM WALKSHITTING TIMES

MSC classification

Primary: 60G50: Sums of independent random variables; random walks
Secondary: 60J55: Local time and additive functionals 60C05: Combinatorial probability
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 4 , December 1995 , pp. 991 - 1006
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by the Alexander von Humboldt Foundation. This work was done while the author was visiting the Carl von Ossietzky University, Oldenburg.

References

Borovkov, A. A. (1976) Stochastic Processes in Queueing Theory. Springer-Verlag, New York.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2. 2nd edn. Wiley, New York.Google Scholar
Jacod, J. and Shiryaev, A. N. (1987) Limit Theorems for Stochastic Processes. Springer-Verlag, Berlin.Google Scholar
Takács, L. (1967) Combinatorial Methods in the Theory of Stochastic Processes. Wiley, New York.Google Scholar
Tallis, G. M. (1962) The use of a generalized multinomial distribution in the estimation of correlation in discrete data. J. R. Statist. Soc. 24, 530–534.Google Scholar
Viskov, O. V. (1970) Some comments on branching processes. Math. Zametki 8, 701–705.Google Scholar