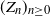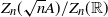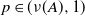Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jiang, Yu
and
Zhang, Shuxiong
2023.
Moderate deviation probabilities for empirical distribution of the branching random walk.
Journal of Mathematical Analysis and Applications,
Vol. 523,
Issue. 1,
p.
126989.
Zhang, Shuxiong
2023.
Lower Deviation Probabilities for Level Sets of the Branching Random Walk.
Journal of Theoretical Probability,
Vol. 36,
Issue. 2,
p.
811.
Zhang, Shuxiong
Liu, Jiawei
and
Xiong, Jie
2025.
Asymptotic expansions in the central limit theorem for a super-Brownian motion.
Bernoulli,
Vol. 31,
Issue. 4,