Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T03:47:26.543Z Has data issue: false hasContentIssue false
  • English
  • Français

On redundancy allocations in systems

Part of: Survival analysis and censored data Operations research and management science

Published online by Cambridge University Press:  14 July 2016

Harshinder Singh  and
Neeraj Misra
Harshinder Singh
Affiliation:
Panjab University
Neeraj Misra*
Affiliation:
Panjab University
*
∗Postal address: Department of Statistics, Panjab University, Chandigarh, India.
Get access Rights & Permissions [Opens in a new window]

Abstract

Allocation of a redundant component in a system in order to optimize, in some sense, the lifetime of the system is an important problem in reliability theory, having practical applications. Consider a series system consisting of two components (say C1 and C2), having independent random lifetimes X1 and X2, and suppose a component C having random lifetime X (independent of X1 and X2) is available for active redundancy with one of the components. Let U1 = min(max(X1, X), X2) and U2 = min(X1, max(X2, X)), so that U1 (U2) denote the lifetime of a system obtained by allocating C to C1 (C2). We consider the criterion where C1 is preferred to C2 for redundancy allocation if . 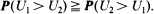Here we investigate the problem of allocating C to C1 or C2, with respect to the above criterion. We also consider the standby redundancy for series and parallel systems with respect to the above criterion. The problem of allocating an active redundant component in order that the resulting system has the smallest failure rate function is also considered and it is observed that unlike stochastic optimization, here the lifetime distribution of the redundant component also plays a role, making the problem of even active redundancy allocation more complex.

Keywords

ACTIVE REDUNDANCYSTANDBY REDUNDANCYORDER STATISTICFAILURE RATE ORDERINGUPSIDE-DOWN BATHTUB-SHAPED FAILURE RATE FUNCTION

MSC classification

Primary: 62N05: Reliability and life testing
Secondary: 90B25: Reliability, availability, maintenance, inspection
Type
Research Article
Information
Journal of Applied Probability , Volume 31 , Issue 4 , December 1994 , pp. 1004 - 1014
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barlow, R. E. and Proschan, F. (1981) Statistical Theory of Reliability and Life Testing: Probability Models. To Begin With, Silver Spring, MD.Google Scholar
Blyth, C. R. (1972) Some probability paradoxes in choice from among random alternatives. J. Amer. Statist. Assoc. 67, 366–373.CrossRefGoogle Scholar
Boland, P. J., El-Neweihi, E. and Proschan, F. (1988) Active redundancy allocation in coherent systems. Prob. Eng. Inf. Sci. 2, 343–353.Google Scholar
Boland, P. J., El-Neweihi, E. and Proschan, F. (1991) Redundancy importance and allocation of spares in coherent systems. J. Statist. Planning. Inf. 29, 55–66.Google Scholar
Boland, P. J., El-Neweihi, E. and Proschan, F. (1992) Stochastic order for redundancy allocations in series and parallel systems. Adv. Appl. Prob. 24, 161–171.Google Scholar
Boland, P. J., El-Neweihi, E. and Proschan, F. (1994) Applications of the hazard rate ordering in reliability. J. Appl. Prob. 31, 188–192.Google Scholar
Bray, T., Crawford, G. and Proschan, F. (1967) Maximum likelihood estimation of a U-shaped failure rate function. Math. Note. 534, Boeing Research Laboratories, Seattle, WA.Google Scholar
Glaser, R. E. (1980) Bathtub and related failure rate characterizations. J. Amer. Statist. Assoc. 75, 667–672.Google Scholar
Lehmann, E. L. (1986) Testing Statistical Hypotheses. 2nd edn. Wiley, Singapore.Google Scholar
Rajarshi, M. B. and Rajarshi, S. M. (1988) Bathtub distributions. A review. Commun. Statist.-Theory Methods 17, 2597–2622.Google Scholar
Ross, S. M. (1983) Stochastic Processes . Wiley, New York.Google Scholar
Shaked, M. and Shanthikumar, J. G. (1992) Optimal allocation of resources to nodes of parallel and series systems. Adv. Appl. Prob. 24, 894–914.Google Scholar
Singh, H. (1989) On partial orderings of life distributions. Naval. Res. Logist. 36, 103–110.Google Scholar