Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T06:50:45.923Z Has data issue: false hasContentIssue false
  • English
  • Français

On resampling schemes for polytopes

Part of: Nonparametric inference

Published online by Cambridge University Press:  11 December 2019

Weinan Qi  and
Mahmoud Zarepour
Weinan Qi*
Affiliation:
University of Ottawa
Mahmoud Zarepour*
Affiliation:
University of Ottawa
*
* Postal address: Department of Mathematics and Statistics, University of Ottawa, Canada.
* Postal address: Department of Mathematics and Statistics, University of Ottawa, Canada.
Get access Rights & Permissions [Opens in a new window]

Abstract

The convex hull of a sample is used to approximate the support of the underlying distribution. This approximation has many practical implications in real life. To approximate the distribution of the functionals of convex hulls, asymptotic theory plays a crucial role. Unfortunately most of the asymptotic results are computationally intractable. To address this computational intractability, we consider consistent bootstrapping schemes for certain cases. Let 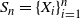$S_n=\{X_i\}_{i=1}^{n}$ be a sequence of independent and identically distributed random points uniformly distributed on an unknown convex set in 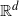$\mathbb{R}^{d}$ ($d\ge 2$ ). We suggest a bootstrapping scheme that relies on resampling uniformly from the convex hull of 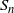$S_n$ . Moreover, the resampling asymptotic consistency of certain functionals of convex hulls is derived under this bootstrapping scheme. In particular, we apply our bootstrapping technique to the Hausdorff distance between the actual convex set and its estimator. For 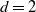$d=2$ , we investigate the asymptotic consistency of the suggested bootstrapping scheme for the area of the symmetric difference and the perimeter difference between the actual convex set and its estimate. In all cases the consistency allows us to rely on the suggested resampling scheme to study the actual distributions, which are not computationally tractable.

Keywords

Convex hullrandom polytopesbootstrapasymptotic

MSC classification

Primary: 62G09: Resampling methods
Secondary: 62G20: Asymptotic properties 62G32: Statistics of extreme values; tail inference
Type
Research Papers
Information
Journal of Applied Probability , Volume 56 , Issue 4 , December 2019 , pp. 959 - 980
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnett, V. (1976). The ordering of multivariate data. J. R. Statist. Soc. A 139, 318–355.CrossRefGoogle Scholar
Bickel, P. J. and Freedman, D. (1981). Some asymptotic theory for the bootstrap. Ann. Statist. 9, 1196–1217.CrossRefGoogle Scholar
Billingsley, P. (1999). Convergence of Probability Measures, 2nd edn. John Wiley, Chichester.CrossRefGoogle Scholar
Bräker, H., Hsing, T. and Bingham, N. H. (1998). On the Hausdorff distance between a convex set and an interior random convex hull. Adv. Appl. Prob. 30, 295–316.CrossRefGoogle Scholar
Bräker, H. and Hsing, T. (1998). On the area and perimeter of a random convex hull in a bounded convex set. Prob. Theory Relat. Fields 111, 517–550.Google Scholar
Cabo, A. J. and Groeneboom, P. (1994). Limit theorems for functionals of convex hulls. Prob. Theory Relat. Fields 100, 31–55.CrossRefGoogle Scholar
Efron, B. (1979). Bootstrap methods: Another look at the jackknife. Ann. Statist. 7, 1–26.CrossRefGoogle Scholar
Hsu, P. L. and Robbins, H. (1974). Complete convergence and the law of large numbers. Proc. Nat. Acad. Sci. USA 33, 25–31.CrossRefGoogle Scholar
Kallenberg, O. (1983). Random Measures, 3rd edn. Akademie, Berlin.Google Scholar
Kobayashi, S. and Nomizu, K. (1996). Foundations of Differential Geometry. Wiley-Interscience, New York.Google Scholar
Liu, R. Y., Parelius, J. M. and Singh, K. (1999). Multivariate analysis by data depth: Descriptive statistics, graphics and inference (with discussion and a rejoinder by Liu and Singh). Ann. Statist. 3, 783–858.Google Scholar
MacDonald, D. W., Ball, F. G. and Hough, N. G. (1980). The evaluation of home range size and configuration using radio tracking data. In A Handbook on Biotelemetry and Radio Tracking, eds MacDonald, D. W. and Amlaner, C. J., Pergamon Press, Oxford.Google Scholar
Reitzner, M. (2005). Central limit theorems for random polytopes. Prob. Theory Relat. Fields 133, 483–507.CrossRefGoogle Scholar
Resnick, S. I. (1987). Extreme Values, Regular Variation and Point Processes. Springer, New York.CrossRefGoogle Scholar
Ripley, B. D. and Rasson, J. P. (1977). Finding the edge of a Poisson forest. J. Appl. Prob. 14, 483–491.CrossRefGoogle Scholar
Schütt, C. (1994). Random polytopes and affine surface area. Math. Nachr. 170, 227–249.CrossRefGoogle Scholar
Tukey, J. W. (1974). Mathematics and the picturing of data. In Proc. Int. Cong. Math., Vol. 2, pp. 523–532.Google Scholar
Zarepour, M. (1999). Bootstrapping convex hulls. Statist. Prob. Lett. 45, 55–63.CrossRefGoogle Scholar