Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sawyer, Stanley
1977.
On the past history of an allele now known to have frequencyp.
Journal of Applied Probability,
Vol. 14,
Issue. 3,
p.
439.
Levikson, Benny
1977.
The age distribution of Markov processes.
Journal of Applied Probability,
Vol. 14,
Issue. 3,
p.
492.
Pakes, Anthony G.
1978.
On the maximum and absorption time of left-continuous random walk.
Journal of Applied Probability,
Vol. 15,
Issue. 02,
p.
292.
Tavaré, S.
1979.
Time reversion and age distributions.
Advances in Applied Probability,
Vol. 11,
Issue. 1,
p.
10.
Tavaré, S.
1979.
Dual diffusions, killed diffusions, and the age distribution problem in population genetics.
Theoretical Population Biology,
Vol. 16,
Issue. 3,
p.
253.
Pakes, Anthony G.
1979.
The age of a Markov process.
Stochastic Processes and their Applications,
Vol. 8,
Issue. 3,
p.
277.
Tavaré, S.
1979.
Time reversion and age distributions.
Advances in Applied Probability,
Vol. 11,
Issue. 01,
p.
10.
Cohn, H.
1979.
Harmonic functions for a class of Markov chains.
Journal of the Australian Mathematical Society,
Vol. 28,
Issue. 4,
p.
413.
Tavaré, S.
1980.
Time reversal and age distributions, I. Discrete-time Markov chains.
Journal of Applied Probability,
Vol. 17,
Issue. 1,
p.
33.
Tavaré, S.
1980.
Time reversal and age distributions, I. Discrete-time Markov chains.
Journal of Applied Probability,
Vol. 17,
Issue. 01,
p.
33.
Kulkarni, M. V.
and
Pakes, A. G.
1983.
The total progeny of a simple branching process with state-dependent immigration.
Journal of Applied Probability,
Vol. 20,
Issue. 03,
p.
472.
Mitov, K. V.
Vatutin, V. A.
and
Yanev, N. M.
1984.
Continuous-time branching processes with decreasing state-dependent immigration.
Advances in Applied Probability,
Vol. 16,
Issue. 04,
p.
697.
Mitov, K. V.
and
Yanev, N. M.
1984.
Critical Galton–Watson processes by decreasing state-dependent immigration.
Journal of Applied Probability,
Vol. 21,
Issue. 01,
p.
22.
Mitov, K. V.
and
Yanev, N. M.
1985.
Bellman–Harris branching processes with state-dependent immigration.
Journal of Applied Probability,
Vol. 22,
Issue. 04,
p.
757.
Griffiths, R. C.
and
Pakes, Anthony G.
1988.
An infinite-alleles version of the simple branching process.
Advances in Applied Probability,
Vol. 20,
Issue. 3,
p.
489.
Mitov, K. V.
and
Yanev, N. M.
1989.
Bellman-Harris branching processes with a special type of state-dependent immigration.
Advances in Applied Probability,
Vol. 21,
Issue. 2,
p.
270.
1993.
Correction.
Journal of Applied Probability,
Vol. 30,
Issue. 02,
p.
496.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
Kesten, Harry
1995.
A ratio limit theorem for (sub) Markov chains on {1,2, …} with bounded jumps.
Advances in Applied Probability,
Vol. 27,
Issue. 03,
p.
652.
Mitov, Kosto V.
1995.
Branching Processes.
Vol. 99,
Issue. ,
p.
47.

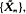 obtained by restarting the original chain at a fixed state after each absorption. The limiting age,
obtained by restarting the original chain at a fixed state after each absorption. The limiting age, 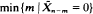 given
given 