Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T18:58:39.195Z Has data issue: false hasContentIssue false
  • English
  • Français

On the asymptotic joint distribution of the sum and maximum of stationary normal random variables

Part of: Stochastic processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

Hwai-Chung Ho  and
Tailen Hsing
Hwai-Chung Ho*
Affiliation:
Academia Sinica
Tailen Hsing*
Affiliation:
Texas A&M University
*
∗Postal address: Institute of Statistical Science, Academia Sinica, Taipei, Taiwan, Republic of China.
∗∗Postal address: Department of Statistics, Texas A&M University, College Station, Texas 77843–3143, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

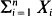Let X1, X2, ·· ·be stationary normal random variables with ρn = cov(X0, Xn). The asymptotic joint distribution of and 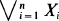is derived under the condition 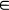ρn log n → γ [0,∞). It is seen that the two statistics are asymptotically independent only if γ = 0.

Keywords

GAUSSIAN PROCESSEXTREME VALUEPARTIAL SUMLONG-RANGE DEPENDENCE

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 60F05: Central limit and other weak theorems 60G15: Gaussian processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 33 , Issue 1 , March 1996 , pp. 138 - 145
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research of Tailen Hsing supported by NAVY-ONR Grant N00014-92-J-1007.

References

Anderson, C. W. and Turkman, K. F. (1991a) The joint limiting distribution of sums and maxima of stationary sequences. J. Appl. Prob. 28, 33–44.Google Scholar
Anderson, C. W. and Turkman, K. F. (1991b). Sums and maxima in stationary sequences. J. Appl. Prob. 28, 715–716.Google Scholar
Beran, J. (1992) Statistical methods for data with long range dependence. Statist. Sci. 7, 404–427.Google Scholar
Berman, S. (1964) Limit theorems for the maximum term in stationary sequences. Ann. Math. Statist. 35, 502–516.CrossRefGoogle Scholar
Chow, T. L. and Teugels, J. L. (1978) The sum and the maximum of i.i.d. random variables. In Proc. Second Prague Symp. Asymptotic Statistics. pp. 81–92.Google Scholar
Hsing, T. (1995) A note on the asymptotic independence of the sum and maximum of strongly mixing stationary random variables. Ann. Prob. 23, 938–947.Google Scholar
Leadbetter, M. R., Lingren, G. and Rootzen, H. (1983) Extremes and Related Properties of Stationary Sequences and Processes. Springer, Berlin.Google Scholar
Mccormick, W. P. and Sun, J. (1993) Sums and maxima of discrete stationary processes. J. Appl. Prob. 30, 863–876.Google Scholar
Mittal, Y. and Ylvisaker, D. (1975) Limit distributions for the maximum of stationary Gaussian processes. Stoch. Proc. Appl. 3, 1–18.Google Scholar
Robinson, P. M. (1993) Times series with strong dependence. In Advances in Econometrics: 6th World Congress. Cambridge University Press, Cambridge.Google Scholar
Rosenblatt, M. (1961) Independence and dependence. Proc. Fourth Berkeley Symp. Math. Statist. Prob. pp. 431–443. University of California Press, Berkeley, CA.Google Scholar