Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Azaïs, Jean-Marc
Cierco-Ayrolles, Christine
and
Croquette, Alain
1999.
Bounds and asymptotic expansions for the distribution of the Maximum of a smooth stationary Gaussian process.
ESAIM: Probability and Statistics,
Vol. 3,
Issue. ,
p.
107.
Adler, Robert J.
2000.
On excursion sets, tube formulas and maxima of random fields.
The Annals of Applied Probability,
Vol. 10,
Issue. 1,
Nadarajah, Saralees
2003.
Stochastic Processes: Modelling and Simulation.
Vol. 21,
Issue. ,
p.
607.
Taylor, Jonathan
Takemura, Akimichi
and
Adler, Robert J.
2005.
Validity of the expected Euler characteristic heuristic.
The Annals of Probability,
Vol. 33,
Issue. 4,
Falk, Michael
Hüsler, Jürg
and
Reiss, Rolf-Dieter
2011.
Laws of Small Numbers: Extremes and Rare Events.
p.
357.
Tan, Zhongquan
2013.
An almost sure limit theorem for the maxima of smooth stationary Gaussian processes.
Statistics & Probability Letters,
Vol. 83,
Issue. 9,
p.
2135.
Cousin, Alexis
Garnier, Josselin
Guiton, Martin
and
Munoz Zuniga, Miguel
2022.
A two-step procedure for time-dependent reliability-based design optimization involving piece-wise stationary Gaussian processes.
Structural and Multidisciplinary Optimization,
Vol. 65,
Issue. 4,

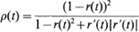
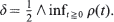 . We give bounds which are roughly of order
. We give bounds which are roughly of order 