Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T14:35:32.616Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Sn/n problem

Part of: Stochastic processes

Published online by Cambridge University Press:  17 May 2022

Sören Christensen  and
Simon Fischer
Sören Christensen*
Affiliation:
Christian-Albrechts-Universität zu Kiel
Simon Fischer*
Affiliation:
Christian-Albrechts-Universität zu Kiel
*
*Postal address: Heinrich-Hecht-Platz 6, D-24118 Kiel, Germany.
*Postal address: Heinrich-Hecht-Platz 6, D-24118 Kiel, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

The Chow–Robbins game is a classical, still partly unsolved, stopping problem introduced by Chow and Robbins in 1965. You repeatedly toss a fair coin. After each toss, you decide whether you take the fraction of heads up to now as a payoff, otherwise you continue. As a more general stopping problem this reads 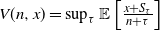$V(n,x) = \sup_{\tau }\mathbb{E} \left [ \frac{x + S_\tau}{n+\tau}\right]$ , where S is a random walk. We give a tight upper bound for V when S has sub-Gaussian increments by using the analogous time-continuous problem with a standard Brownian motion as the driving process. For the Chow–Robbins game we also give a tight lower bound and use these to calculate, on the integers, the complete continuation and the stopping set of the problem for 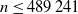$n\leq 489\,241$ .

Keywords

Brownian motionChow–Robbins gameoptimal stoppingupper boundlower bound

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 60G50: Sums of independent random variables; random walks
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 2 , June 2022 , pp. 571 - 583
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chow, Y. S. and Robbins, H. (1965). On optimal stopping rules for $s_{n}/n$ . Illinois J. Math. 3, 444–454.Google Scholar
Christensen, S. and Fischer, S. (2020). Note on the (non-)smoothness of discrete time value functions in optimal stopping. Electron. Commun. Prob. 25, 1–10.10.1214/20-ECP335CrossRefGoogle Scholar
Dvoretzky, A. (1967). Existence and properties of certain optimal stopping rules. In Proc. Fifth Berkeley Symp. Math. Statist. Prob., Vol. 1, University of California Press, Berkeley, pp. 441–452.Google Scholar
Häggström, O. and Wästlund, J. (2013). Rigorous computer analysis of the Chow–Robbins game. Amer. Math. Monthly 120, 893–900.CrossRefGoogle Scholar
Leung Lai, T. and Yao, Y.-C. (2005). The optimal stopping problem for $\frac{S_n}{n}$ and its ramifications. Tech. Rep. 2005-22, Department of Statistics, Stanford University.Google Scholar
Leung Lai, T., Yao, Y.-C. and Aitsahlia, F. (2007). Corrected random walk approximations to free boundary problems in optimal stopping. Adv. Appl. Prob. 39, 753–775.Google Scholar
Medina, L. A. and Zeilberger, D. (2009). An experimental mathematics perspective on the old, and still open, question of when to stop. Preprint, arXiv:0907.0032.Google Scholar
Peskir, G. and Shiryaev, A. (2006). Optimal Stopping and Free-Boundary Problems. Birkhäuser Basel.Google Scholar
Shepp, L. A. (1969). Explicit solutions to some problems of optimal stopping. Ann. Math. Statist. 40, 993–1010.CrossRefGoogle Scholar
Walker, L. H. (1969). Regarding stopping rules for Brownian motion and random walks. Bull. Amer. Math. Soc. 75, 46–50.10.1090/S0002-9904-1969-12140-3CrossRefGoogle Scholar