Optimal control of a finite dam: average-cost case

Abstract

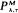We consider the problem of minimizing the long-run average cost per unit time of operating a finite dam in the class of the policies of the following type. Assume that the dam is initially empty, the release rate is kept at 0 until the dam storage increases to λ, and as soon as this occurs, water is released at rate M, then the output rate is kept at M as long as the dam storage is more than τ and it must be decreased to 0 if the dam storage becomes τ. We assume that the input of water into the finite dam is a Wiener process with non-negative drift μ and variance parameter σ². There is a cost in increasing the output rate from 0 to M as well as in decreasing the rate from M to 0 and whenever the dam storage is below level a, there is a penalty cost per unit time depending on the level. A reward is given for each unit of water released. In this paper, the long-run average cost per unit time is determined, and therefore the optimal policy 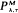can be found numerically.