Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T13:09:14.917Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal estimation for semimartingales

Published online by Cambridge University Press:  14 July 2016

A. Thavaneswaran  and
M. E. Thompson
A. Thavaneswaran*
Affiliation:
University of Waterloo
M. E. Thompson*
Affiliation:
University of Waterloo
*
∗Postal address: Department of Statistics and Actuarial Science, Faculty of Mathematics, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1.
∗Postal address: Department of Statistics and Actuarial Science, Faculty of Mathematics, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper extends a result of Godambe's theory of parametric estimation for discrete-time stochastic processes to the continuous-time case. Let P ={P} be a family of probability measures such that (Ω, F, P) is complete, (Ft, t≧0) is a standard filtration, and X = (Xt Ft, t ≧ 0) is a semimartingale for every P ∈ P. For a parameter θ (Ρ), suppose Xt = Vt,θ + Ht,θ where the Vθ process is predictable and locally of bounded variation and the Hθ process is a local martingale. 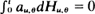Consider estimating equations for θ of the form process is predictable. Under regularity conditions, an optimal form for α θ in the sense of Godambe (1960) is determined. When Vt,θ is linear in θ the optimal 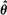, corresponds to certain maximum likelihood or least squares estimates derived previously in special cases. Asymptotic properties of 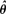, are discussed.

Keywords

ESTIMATING FUNCTIONS: STOCHASTIC INTEGRALS
Type
Research Paper
Information
Journal of Applied Probability , Volume 23 , Issue 2 , June 1986 , pp. 409 - 417
Copyright
Copyright © Applied Probability Trust 1986 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aalen, O. O. (1978) Nonparametric inference for a family of counting processes. Ann. Statist. 6, 701–726.Google Scholar
Aase, K. K. (1981) Model reference adaptive systems applied to regression theory. Statist. Neerlandica 3, 129–155.Google Scholar
Aase, K. K. (1982) Stochastic continuous-time model reference adaptive systems with decreasing gain. Adv. Appl. Prob. 14, 763–788.Google Scholar
Aase, K. K. (1983) Recursive estimation in nonlinear time series models of autoregressive type. J. R. Statist. Soc. B 45, 228–237.Google Scholar
Elliot, R. J. (1982) Stochastic Calculus and Applications. Springer-Verlag, New York.Google Scholar
Feigin, P. D. (1976) Maximum likelihood estimation for continuous time stochastic processes. Adv. Appl. Prob. 8, 712–736.Google Scholar
Ferreira, P. E. (1982) Estimating equations in the presence of prior knowledge. Biometrika 69, 667–669.Google Scholar
Godambe, V. P. (1960) An optimum property of regular maximum likelihood estimation. Ann. Math. Statist. 31, 1208–1211.Google Scholar
Godambe, V. P. (1985) The foundations of finite sample estimation in stochastic processes. Biometrika 72, 419–428.CrossRefGoogle Scholar
Grenander, U. (1981) Abstract Inference. Wiley, New York.Google Scholar
Kunita, H. and Watanabe, S. (1967) On square integrable martingales. Nagoya Math. J. 30, 209–245.CrossRefGoogle Scholar
Liptser, R. S. (1980) A strong law of large numbers for local martingales. Stochastics 3, 217–228.Google Scholar
Liptser, R. S. and Shiryayev, A. N. (1977) Statistics of Random Processes, 2. Springer-Verlag, New York.Google Scholar
Liptser, R. S. and Shiryayev, A. N. (1980) A functional central limit theorem for semimartingales. Theory Prob. Appl. 25, 667–688.Google Scholar
Mckean, H. P. Jr. (1969) Stochastic Integrals. Academic Press, New York.Google Scholar
Metivier, M. (1982) Semimartingales. Walter de Gruyter, New York.Google Scholar
Segall, A. (1973) A Martingale Approach to Modelling, Estimation and Detection of Jump Processes. , Stanford University.Google Scholar
Van Shuppen, J. H. (1979) Stochastic Filtering Theory. Springer-Verlag, New York.Google Scholar