Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T21:44:54.582Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal second-order product probability bounds

Part of: Multivariate analysis

Published online by Cambridge University Press:  14 July 2016

Henry W. Block ,
Timothy M. Costigan  and
Allan R. Sampson
Henry W. Block*
Affiliation:
University of Pittsburgh
Timothy M. Costigan*
Affiliation:
The Ohio State University
Allan R. Sampson*
Affiliation:
University of Pittsburgh
*
∗ Postal address: Department of Mathematics and Statistics, University of Pittsburgh, PA 15260, USA.
∗∗ Postal address: Department of Statistics, The Ohio State University, 141 Cockins Hall, Columbus, OH 43210-1247, USA.
∗ Postal address: Department of Mathematics and Statistics, University of Pittsburgh, PA 15260, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let P(c) = P(X1 ≦ c1, · ··, Xp ≦ cp) for a random vector (X1, · ··, Xp). Bounds are considered of the form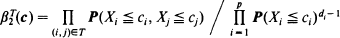 where T is a spanning tree corresponding to the bivariate probability structure and di is the degree of the vertex i in T. An optimized version of this inequality is obtained. The main result is that 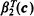alwayṡ dominates certain second-order Bonferroni bounds. Conditions on the covariance matrix of a N(0,Σ) distribution are given so that this bound applies, and various applications are given.

Keywords

PRODUCT BOUNDSSECOND-ORDER BOUNDSBONFERRONI BOUNDSMTP2PARTIAL CORRELATIONPOSITIVE DEPENDENCEGRAPH THEORYCHANGE POINTSIMULTANEOUS INFERENCE

MSC classification

Primary: 62H05: Characterization and structure theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 3 , September 1993 , pp. 675 - 691
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by NSA Grant No. MDA-904-90-H-4063 and by the Air Force Office of Scientific Research under Contract AFOSR 84-0113.

Research supported by NCI Grant No. 1-R01-CA54706-01, by the Air Force Office of Scientific Research under Contract AFOSR 84-0113, and by a seed grant from the Ohio State University.

References

Bauer, P. (1986a) Two stage testing for simultaneously testing main and side effects in clinical trials. Biometrical J. 27, 25–38.Google Scholar
Bauer, P. (1986b) Approximation of discrete boundaries. Biometrika 73, 759–760.Google Scholar
Bauer, P. and Hackl, P. (1985) The application of Hunter's inequality in simultaneous testing. Biometrical J. 27, 25–38.Google Scholar
Bjornstadt, J. F. and Butler, R. W. (1988) The equivalence of backward elimination and multiple comparisons. J. Amer. Statist. Assoc. 83, 136–144.Google Scholar
Block, H.W., Costigan, T. and Sampson, A. R. (1990) Second order lower and upper probability bounds. Submitted for publication.Google Scholar
Block, H. W., Costigan, T. and Sampson, A. R. (1992) Product-type probability bounds of higher order. Prob. Eng. Inf. Sci. 6, 349–370.Google Scholar
Bolviken, E. (1982) Probability inequalities for the multivariate normal with non-negative partial correlations. Scand. J. Statist. 9, 49–58.Google Scholar
Costigan, T. (1992a) Optimal Bonferroni and product-type probability bounds of the first three orders. Submitted for publication.Google Scholar
Costigan, T. (1992b) An overview of probability inequalities emphasizing nested Bonferroni-type bounds with strategies for their use. Submitted for publication.Google Scholar
Cunrow, E. A. and Dunnett, C. W. (1963) The numerical evaluation of certain multivariate normal integrals. Ann. Math. Statist. 33, 571–579.Google Scholar
Dunnett, C. W. (1955) A multiple comparison procedure for comparing several treatments with a control. J. Amer. Statist. Assoc. 50, 1096–1121.Google Scholar
Glaz, J. (1989) Approximations and bounds for the distribution of the scan statistic. J. Amer. Statist. Assoc. 84, 560–566.Google Scholar
Glaz, J. (1990) A comparison of Bonferroni-type and product-type inequalities in presence of dependence. Topics in Statistical Dependence, ed. Block, H. W., Sampson, A. R. and Savits, T. H. IMS Lecture Monograph Series.Google Scholar
Glaz, J. and Johnson, B. Mck. (1984) Probability inequalities for multivariate distributions with dependence structures. J. Amer. Statist. Assoc. 79, 436–441.Google Scholar
Graybill, F. A. (1983) Matrices with Applications in Statistics. Wadsworth, Belmont, CA.Google Scholar
Gupta, S. H. (1963) Probability integrals of multivariate normal and multivariatet. Ann. Math. Statist. 34, 792–828.Google Scholar
Hoover, D. R. (1990a) Comparison of improved Bonferroni and Sidak/Slepian bounds with applications to normal Markov processes. Commun. Statist. 19, 1623–37.Google Scholar
Hoover, D. R. (1990b) Subset complement addition upper bounds - An improved inclusion-exclusion method. J. Statist. Planning Inf. 12, 195–202.Google Scholar
Hunter, D. (1976) An upper bound for the probability of a union. J. Appl. Prob. 13, 597–603.Google Scholar
Karlin, S. and Rinott, Y. (1980a) Classes of orderings of measures and related correlation inequalities - I: Multivariate totally positive distributions. J. Multivariate Anal. 10, 476–498.Google Scholar
Karlin, S. and Rinott, Y. (1980b) Classes of orderings of measures and related correlation inequalities - II: Multivariate reverse rule distributions. J. Multivariate Anal. 10, 499–516.Google Scholar
Karlin, S. and Rinott, Y. (1982) Total positivity properties of absolute value multinormal distributions with applications to confidence interval estimates and related probabalistic inequalities. Ann. Statist. 9, 1035–1049.Google Scholar
Karlin, S. and Rinott, Y. (1983) M-matrices as covariance matrices of multinormal distributions. Linear Algebra Appl. 52/53, 419–438.Google Scholar
Kounias, E. G. (1968) Bounds for the probability of a union. Ann. Math. Statist. 39, 2154–2158.Google Scholar
Kruskal, J. B. (1956) On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Amer. Math. Soc. 7, 48–50.Google Scholar
Pocock, S. J. (1977) Group sequential methods in the design and analysis of clinical trials. Biometrika 64, 191–199.Google Scholar
Ravishanker, N., Hochberg, Y. and Melnick, E. L. (1987) Approximate simultaneous prediction intervals for multiple forecasts. Technometrics 29, 371–376.Google Scholar
Seneta, E. (1988) Degree, iteration and permutation in improving Bonferroni-type bounds. Austral. J. Statist. 30A, 27–38.Google Scholar
Stoline, M.R. (1983) The Hunter method of simultaneous inference and its recommended use for applications having large known correlation structure. J. Amer. Statist. Assoc. 78, 366–370.Google Scholar
Tong, Y. L. (1980) Probability Inequalities in Multivariate Distributions. Academic Press, New York.Google Scholar
Worsley, K. J. (1982) ‘An improved Bonferroni inequality and applications.’ Biometrika 69, 297–302.Google Scholar