Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Banks, Jeffrey S.
and
Sundaram, Rangarajan K.
1992.
A class of bandit problems yielding myopic optimal strategies.
Journal of Applied Probability,
Vol. 29,
Issue. 03,
p.
625.
Hamada, Toshio
1992.
A doscounted uniform one-armed bandit problem.
Sequential Analysis,
Vol. 11,
Issue. 1,
p.
1.
Liang, Annie
Mu, Xiaosheng
and
Syrgkanis, Vasilis
2017.
Optimal Learning from Multiple Information Sources.
SSRN Electronic Journal ,

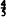 . Moreover,
. Moreover, 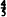 is best possible. The case where the parameters of the beta distribution are arbitrary positive numbers is also treated.
is best possible. The case where the parameters of the beta distribution are arbitrary positive numbers is also treated.