Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Orsingher, Enzo
1987.
Stochastic motions on the 3-sphere governed by wave and heat equations.
Journal of Applied Probability,
Vol. 24,
Issue. 02,
p.
315.
Orsingher, Enzo
1987.
Stochastic motions driven by wave equations.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 57,
Issue. 1,
p.
365.
Dunbar, Steven R.
1988.
A Branching Random Evolution and a Nonlinear Hyperbolic Equation.
SIAM Journal on Applied Mathematics,
Vol. 48,
Issue. 6,
p.
1510.
Orsingher, Enzo
1990.
Probability law, flow function, maximum distribution of wave-governed random motions and their connections with Kirchoff's laws.
Stochastic Processes and their Applications,
Vol. 34,
Issue. 1,
p.
49.
Masoliver, Jaume
Porrà, Josep M.
and
Weiss, George H.
1992.
The continuum limit of a two-dimensional persistent random walk.
Physica A: Statistical Mechanics and its Applications,
Vol. 182,
Issue. 4,
p.
593.
Suppes, Patrick
and
de Barros, J. Acacio
1994.
A random-walk approach to interference.
International Journal of Theoretical Physics,
Vol. 33,
Issue. 1,
p.
179.
Foong, S. K.
1995.
Overcoming dissipative distortions by a waveform restorer and designer.
Journal of Mathematical Physics,
Vol. 36,
Issue. 5,
p.
2324.
García-Colín, L.S.
and
Olivares-Robles, M.A.
1995.
Hyperbolic type transport equations.
Physica A: Statistical Mechanics and its Applications,
Vol. 220,
Issue. 1-2,
p.
165.
Porrà, Josep M.
Weiss, George H.
and
Masoliver, Jaume
1995.
A diffusion model incorporating anisotropic properties.
Physica A: Statistical Mechanics and its Applications,
Vol. 218,
Issue. 1-2,
p.
229.
Olivares-Robles, M. A.
and
García-Colín, L. S.
1996.
On Different Derivations of Telegrapher’s Type Kinetic Equations.
Journal of Non-Equilibrium Thermodynamics,
Vol. 21,
Issue. 4,
Kolesnik, Alexander D.
and
Turbin, Anatoly F.
1998.
The equation of symmetric Markovian random evolution in a plane.
Stochastic Processes and their Applications,
Vol. 75,
Issue. 1,
p.
67.
Márkus, Ferenc
Gambár, Katalin
Vázquez, Federico
and
del Rı́o, J.Antonio
1999.
Classical field theory and stochastic properties of hyperbolic equations of dissipative processes.
Physica A: Statistical Mechanics and its Applications,
Vol. 268,
Issue. 3-4,
p.
482.
Hadeler, K. P.
1999.
Mathematics Inspired by Biology.
Vol. 1714,
Issue. ,
p.
95.
Bondarenko, Yu. V.
2000.
Probabilistic Model for Description of Evolution of Financial Indices.
Cybernetics and Systems Analysis,
Vol. 36,
Issue. 5,
p.
738.
Iacus, Stefano Maria
2001.
Statistical analysis of the inhomogeneous telegrapher's process.
Statistics & Probability Letters,
Vol. 55,
Issue. 1,
p.
83.
Di Crescenzo, Antonio
2002.
Exact transient analysis of a planar random motion with three directions.
Stochastics and Stochastic Reports,
Vol. 72,
Issue. 3-4,
p.
175.
Mathé, Peter
and
Hinrich Zacharias-Langhans, Johann
2003.
Mathematics — Key Technology for the Future.
p.
493.
Vázquez, F.
del Río, J.A.
and
de Haro, M. López
2005.
Variational and Extremum Principles in Macroscopic Systems.
p.
523.
Kolesnik, Alexander D.
and
Orsingher, Enzo
2005.
A planar random motion with an infinite number of directions controlled by the damped wave equation.
Journal of Applied Probability,
Vol. 42,
Issue. 04,
p.
1168.
Plyukhin, A. V.
2010.
Stochastic process leading to wave equations in dimensions higher than one.
Physical Review E,
Vol. 81,
Issue. 2,

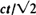 . The explicit density of the particle position is obtained. Results concerning the trend of motion are also given.
. The explicit density of the particle position is obtained. Results concerning the trend of motion are also given.