Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ferrari, P. A.
Martinez, S.
and
San Martín, J.
1997.
Phase transition for absorbed Brownian motion with drift.
Journal of Statistical Physics,
Vol. 86,
Issue. 1-2,
p.
213.
Martinez, Servet
Picco, Pierre
and
San Martin, Jaime
1998.
Domain of attraction of quasi-stationary distributions for the brownian motion with drift.
Advances in Applied Probability,
Vol. 30,
Issue. 02,
p.
385.
Fierro, Raúl
Martínez, Servet
and
San Martín, Jaime
1999.
Limiting conditional and conditional invariant distributions for the Poisson process with negative drift.
Journal of Applied Probability,
Vol. 36,
Issue. 4,
p.
1194.
Fierro, Raúl
Martínez, Servet
and
San Martín, Jaime
1999.
Limiting conditional and conditional invariant distributions for the Poisson process with negative drift.
Journal of Applied Probability,
Vol. 36,
Issue. 04,
p.
1194.
Lladser, Manuel
and
San Martín, Jaime
2000.
Domain of attraction of the quasi-stationary distributions for the Ornstein-Uhlenbeck process.
Journal of Applied Probability,
Vol. 37,
Issue. 2,
p.
511.
Aalen, Odd O.
and
Gjessing, Håkon K.
2001.
Understanding the shape of the hazard rate: a process point of view (With comments and a rejoinder by the authors).
Statistical Science,
Vol. 16,
Issue. 1,
Aalen, Odd O.
2005.
Encyclopedia of Biostatistics.
Kyprianou, Andreas E.
and
Palmowski, Zbigniew
2006.
Quasi-stationary distributions for Lévy processes.
Bernoulli,
Vol. 12,
Issue. 4,
Jun, Ye
2008.
Quasi-stationary distributions for the radial ornstein-uhlenbeck processes.
Acta Mathematica Scientia,
Vol. 28,
Issue. 3,
p.
513.
Бурнаев, Евгений Владимирович
Burnaev, Evgenii Vladimirovich
Файнберг, Евгений А
Feinberg, Eugene A
Ширяев, Альберт Николаевич
and
Shiryaev, Albert Nikolaevich
2008.
Об асимптотической оптимальности второго порядка в минимаксной задаче скорейшего обнаружения момента изменения сноса у броуновского движения.
Теория вероятностей и ее применения,
Vol. 53,
Issue. 3,
p.
557.
Burnaev, E. V.
Feinberg, E. A.
and
Shiryaev, A. N.
2009.
On Asymptotic Optimality of the Second Order in the Minimax Quickest Detection Problem of Drift Change for Brownian Motion.
Theory of Probability & Its Applications,
Vol. 53,
Issue. 3,
p.
519.
Mandjes, Michel
Palmowski, Zbigniew
and
Rolski, Tomasz
2012.
Quasi-Stationary Workload in a Lévy-Driven Storage System.
Stochastic Models,
Vol. 28,
Issue. 3,
p.
413.
Simpson, Gideon
and
Luskin, Mitchell
2013.
Numerical analysis of parallel replica dynamics.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 47,
Issue. 5,
p.
1287.
Collet, Pierre
Martínez, Servet
and
San Martín, Jaime
2013.
Quasi-Stationary Distributions.
p.
113.
Aristoff, D.
Lelievre, T.
and
Simpson, G.
2014.
The Parallel Replica Method for Simulating Long Trajectories of Markov Chains.
Applied Mathematics Research eXpress,
Aalen, Odd O.
2014.
Wiley StatsRef: Statistics Reference Online.
Binder, Andrew
Lelièvre, Tony
and
Simpson, Gideon
2015.
A generalized parallel replica dynamics.
Journal of Computational Physics,
Vol. 284,
Issue. ,
p.
595.
Berestycki, Julien
Berestycki, Nathanaël
and
Schweinsberg, Jason
2015.
Critical branching Brownian motion with absorption: Particle configurations.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 51,
Issue. 4,
Zhang, Hanjun
and
He, Guoman
2016.
Existence and construction of quasi-stationary distributions for one-dimensional diffusions.
Journal of Mathematical Analysis and Applications,
Vol. 434,
Issue. 1,
p.
171.
Zhang, Hanjun
and
He, Guoman
2016.
Domain of attraction of quasi-stationary distribution for one-dimensional diffusions.
Frontiers of Mathematics in China,
Vol. 11,
Issue. 2,
p.
411.

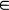 A
A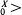 > t
> t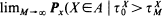 ) which is the law of a Bessel process with drift.
) which is the law of a Bessel process with drift.