Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T21:45:23.221Z Has data issue: false hasContentIssue false
  • English
  • Français

Queues with path-dependent arrival processes

Part of: Operations research and management science Limit theorems Special processes

Published online by Cambridge University Press:  23 June 2021

Kerry Fendick  and
Ward Whitt Open the ORCID record for Ward Whitt [Opens in a new window]
Kerry Fendick*
Affiliation:
Johns Hopkins University Applied Physics Laboratory
Ward Whitt*
Affiliation:
Columbia University
*
*Postal address: Communications Systems Branch, Johns Hopkins University Applied Physics Laboratory, Laurel, MD 20723, USA. Email address: Kerry.Fendick@jhuapl.edu
**Postal address: Department of Industrial Engineering and Operations Research, Columbia University, New York, NY 10027-6699, USA. Email address: ww2040@columbia.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the transient and limiting behavior of a queue with a Pólya arrival process. The Pólya process is interesting because it exhibits path-dependent behavior, e.g. it satisfies a non-ergodic law of large numbers: the average number of arrivals over time [0, t] converges almost surely to a nondegenerate limit as 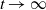$t \rightarrow \infty$. We establish a heavy-traffic diffusion limit for the 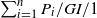$\sum_{i=1}^{n} P_i/GI/1$ queue, with arrivals occurring exogenously according to the superposition of n independent and identically distributed Pólya point processes. That limit yields a tractable approximation for the transient queue-length distribution, because the limiting net input process is a Gaussian Markov process with stationary increments. We also provide insight into the long-run performance of queues with path-dependent arrival processes. We show how Little’s law can be stated in this context, and we provide conditions under which there is stability for a queue with a Pólya arrival process.

Keywords

path-dependent stochastic processesgeneralized Pólya processGaussian Markov processdiffusion approximationsqueuesheavy-traffic limit

MSC classification

Primary: 60K25: Queueing theory
Secondary: 60F17: Functional limit theorems; invariance principles 90B22: Queues and service
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 2 , June 2021 , pp. 484 - 504
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arthur, W. B. (1988). Self-reinforcing mechanisms in economics. In The Economy as an Evolving Complex System, eds P. W. Anderson, K. Arrow and D. Pines. CRC Press, Boca Raton, FL.Google Scholar
Arthur, W. B., Ermoliev, Yu. M. and Kanjovski, Yu. M (1987). Path-dependent processes and the emergence of macro-structure. Eur. J. Operat. Res. 30, 294–303.CrossRefGoogle Scholar
Baccelli, F. and Bremaud, P. (1994). Elements of Queueing Theory. Springer, New York.Google Scholar
Bacray, E., Delattre, S., Hoffman, M. and Muzy, J. F. (2013). Some limit theorems for Hawkes processes and applications to finanical statistics. Stoch. Process. Appl. 123, 2475–2499.CrossRefGoogle Scholar
Billingsley, P. (1999). Convergence of Probability Measures, 2nd edn. John Wiley, New York.CrossRefGoogle Scholar
Breiman, L. (1968). Probability. Addison Wesley, Reading, MA.Google Scholar
Cha, J. H. (2014). Characterization of the generalized Pólya process and its applications. Adv. Appl. Prob. 46, 1148–1171.10.1239/aap/1418396247CrossRefGoogle Scholar
Cha, J. H. and Badia, F. G. (2019). On a multivariate generalized Pólya process without regularity property. Prob. Eng. Inf. Sci. 34, 484–506.CrossRefGoogle Scholar
Daw, A. and Pender, J. (2018). Queues driven by Hawkes processes. Stoch. Systems 8, 192–229.CrossRefGoogle Scholar
Debicki, K. and Rolski, T. (2002). A note on transient Gaussian fluid models. Queueing Systems 41, 321–342.10.1023/A:1016283330996CrossRefGoogle Scholar
Debicki, K., Kosinski, K. and Mandjes, M. (2012). Gaussian queues in light and heavy traffic. Queueing Systems 71, 137–149.10.1007/s11134-011-9270-xCrossRefGoogle Scholar
Doob, J. L. (1953). Stochastic Processes, Wiley, New York.Google Scholar
Ethier, S. N. and Kurtz, T. G. (1986). Markov Processes: Characterization and Convergence, Wiley, New York.10.1002/9780470316658CrossRefGoogle Scholar
Feller, W. (1968). An Introduction to Probability Theory and its Applications, Vol. I, 3rd edn. John Wiley, New York.Google Scholar
Feller, W. (1971). An Introduction to Probability Theory and its Applications, Vol. II, 2nd edn. John Wiley, New York.Google Scholar
Fendick, K. W. (2020). Brownian motion minus the independent increments: Representation and queuing application. Prob. Eng. Inf. Sci., doi: 10.1017/S0269964820000388.CrossRefGoogle Scholar
Fendick, K. W. and Whitt, W. (1989). Measurements and approximations to describe the offered traffic and predict the average workload in a single-server queue. Proc. IEEE 71, 171–194.10.1109/5.21078CrossRefGoogle Scholar
Gao, X. and Zhu, L. (2018). Functional central limit theorems for stationary Hawkes processes and application to infinite-server queues. Queueing Systems 90, 161–206.10.1007/s11134-018-9570-5CrossRefGoogle Scholar
Glynn, P. W. and Whitt, W. (1991). A new view of the heavy-traffic limit for infinite-server queues. Adv. Appl. Prob. 23, 188–209.CrossRefGoogle Scholar
Gregoire, G. (1983). Negative binomial distributions for point processes. Stochastic Proc. Appl. 16, 179–188.CrossRefGoogle Scholar
Hahn, M. G. (1978). Central limit theorems in D[0,1]. Z. Wahrscheinlichkeitsth. 44, 89–101.CrossRefGoogle Scholar
Hajek, B. (1994). A queue with periodic arrivals and constant service. In Probability, Statistics and Optimization: A Tribute to Peter Whittle, ed. F. P. Kelley. Wiley, Chichester, pp. 147–157.Google Scholar
Hawkes, A. G. (1971a). Spectra of some self-exciting and mutually exciting point processes. Biometrika 58, 83–90.CrossRefGoogle Scholar
Hawkes, A. G. (1971b). Point spectra of some mutually exciting point processes. J. R. Statist. Soc. 33, 438–443.Google Scholar
Honnappa, H., Jain, R. and Ward, A. (2015). A queueing model with independent arrivals and its fluid and diffusion limits. Queueing Systems 80, 71–103.10.1007/s11134-014-9428-4CrossRefGoogle Scholar
Isaacson, D. and Madsen, R. (1976). Markov Chains: Theory and Applications. Wiley, New York.Google Scholar
Konno, T. H (2010). On the exact solution of a generalized Polya process. Adv. Math. Phys. 2010, 504267.10.1155/2010/504267CrossRefGoogle Scholar
Li, A. and Whitt, W. (2014). Approximate blocking probabilities for loss models with independence and distribution assumptions relaxed. Performance Evaluation 80, 82–101.CrossRefGoogle Scholar
Liu, Y. and Whitt, W. (2011). Large-time asymptotics for the $G_{t}/M_{t}/s_{t} + GI_{t}$ many-server fluid model with customer abandonment. Queueing Systems 67, 145–182.CrossRefGoogle Scholar
Ma, N. and Whitt, W. (2019). Minimizing the maximum expected waiting time in a periodic single-server queue with a service-rate control. Stochastic Systems 9, 261–290.CrossRefGoogle Scholar
Mirtchev, S. T. (2019). Study of preemptive priority single-server queue with peaked arrival flow. In Proc. X Nat. Conf. with Int. Participation ‘Electronica 2019’, May 16–17, 2019, Sofia, Bulgaria.Google Scholar
Mirtchev, S. T. and Goleva, R. (2013). New constant service time Pólya $/D/n$ traffic model with peaked input stream. Simul. Model. Pract. Theory 34, 200–207.10.1016/j.simpat.2012.08.004CrossRefGoogle Scholar
Mirtchev, S. T. and Ganchev, I. (2016). Generalised Pollaczek–Khinchin formula for the Pólya $/G/1$ queue. Electron. Lett. 53, 27–29.CrossRefGoogle Scholar
Pólya, G. and Eggenberger, F. (1923). Uber die Statistik verketteter Vorgange. Z. angewandte Mathematische Mechanik, 3, 279–289.Google Scholar
Stidham, S. (1974). A last word on $L = \lambda W$. Operat. Res. 22, 417–421.CrossRefGoogle Scholar
Whitt, W. (2002). Stochastic Process Limits. Springer, New York.10.1007/b97479CrossRefGoogle Scholar
Whitt, W. (2015). Stabilizing performance in a single-server queue with time-varying arrival rate. Queueing Systems 81, 341–378.CrossRefGoogle Scholar
Whitt, W. and You., W. (2018). Using robust queueing to expose the impact of dependence in single-server queues. Operat. Res. 66, 184–199.CrossRefGoogle Scholar
Whitt, W. and You., W. (2019). The advantage of indices of dispersion in queueing approximations. Operat. Res. Lett. 47, 99–104.CrossRefGoogle Scholar
Wolff, R. W. and Yao, Y. (2014). Little’s law when the average waiting time is infinite. Queueing Systems 76, 267–281.10.1007/s11134-013-9364-8CrossRefGoogle Scholar