Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Takács, Lajos
1981.
Random Flights on Regular Polytopes.
SIAM Journal on Algebraic Discrete Methods,
Vol. 2,
Issue. 2,
p.
153.
Letac, Gérard
1982.
Les fonctions sphériques d'un couple de Gelfand symétrique et les chaînes de Markov.
Advances in Applied Probability,
Vol. 14,
Issue. 2,
p.
272.
van Slijpe, A.R.D.
1984.
RANDOM WALKS ON REGULAR POLYHEDRA AND OTHER DISTANCE–REGULAR GRAPHS.
Statistica Neerlandica,
Vol. 38,
Issue. 4,
p.
273.
Ycart, Bernard
1984.
L'application des representations au calcul explicite sur certaines chaînes de Markov finies.
Advances in Applied Probability,
Vol. 16,
Issue. 3,
p.
656.
Aldous, David
and
Diaconis, Persi
1987.
Strong uniform times and finite random walks.
Advances in Applied Mathematics,
Vol. 8,
Issue. 1,
p.
69.
Bingham, N. H.
1991.
Fluctuation Theory for the Ehrenfest urn.
Advances in Applied Probability,
Vol. 23,
Issue. 03,
p.
598.
Bingham, N. H.
1994.
The work of Lajos Takács on probability theory.
Journal of Applied Probability,
Vol. 31,
Issue. A,
p.
29.
Bingham, N.H.
2001.
Stochastic Processes: Theory and Methods.
Vol. 19,
Issue. ,
p.
171.
Shannon, A. G.
and
Ollerton, R. L.
2002.
Combinatorial Matrices and Linear Recursive Sequences.
The Fibonacci Quarterly,
Vol. 40,
Issue. 5,
p.
417.
Ollerton, Richard L.
and
Shannon, Anthony G.
2004.
Applications of Fibonacci Numbers.
p.
187.
Garza-López, Roberto A.
Brzezinski, Jack
and
Kozak, John J.
2012.
Reaction efficiency of diffusion-controlled processes on finite, aperiodic planar lattices – III: Supramolecular architectures.
Chemical Physics Letters,
Vol. 538,
Issue. ,
p.
86.

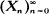 on the vertices of a regular dodecahedron
on the vertices of a regular dodecahedron 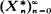 on the oriented edges (
on the oriented edges (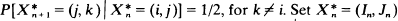 and fix a vertex
and fix a vertex 