Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Heyde, C. C.
1971.
Some central limit analogues for supercritical Galton-Watson processes.
Journal of Applied Probability,
Vol. 8,
Issue. 01,
p.
52.
Iosifescu, M.
and
Tăutu, P.
1973.
Stochastic processes and applications in biology and medicine I.
Vol. 3,
Issue. ,
p.
11.
Bingham, N. H.
and
Doney, R. A.
1974.
Asymptotic properties of supercritical branching processes I: The Galton-Watson process.
Advances in Applied Probability,
Vol. 6,
Issue. 4,
p.
711.
Cohn, Harry
and
Pakes, Anthony G.
1978.
A representation for the limiting random variable of a branching process with infinite mean and some related problems.
Journal of Applied Probability,
Vol. 15,
Issue. 02,
p.
225.
Vatutin, V. A.
and
Zubkov, A. M.
1987.
Branching processes. I.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 1,
p.
2431.
Korolev, V. Yu.
1991.
Nonuniform estimates of the stability of the normal law under random perturbations of the scale parameter and some of their applications.
Journal of Soviet Mathematics,
Vol. 57,
Issue. 4,
p.
3270.
Quine, Malcolm P.
and
Szczotka, Wladystaw
1998.
Asymptotic normality of processes with a branching structure.
Communications in Statistics. Stochastic Models,
Vol. 14,
Issue. 4,
p.
833.
Devroye, Luc
1998.
Probabilistic Methods for Algorithmic Discrete Mathematics.
Vol. 16,
Issue. ,
p.
249.
Uwe, Rösler
Valentin, Topchii
and
Vladimir, Vatutin
2002.
Mathematics and Computer Science II.
p.
441.
Heyde, C. C.
2010.
Selected Works of C.C. Heyde.
p.
138.
Zhenlong, Gao
and
Xiaoyu, Hu
2012.
Limit theorems for a galton-watson process in the I.I.D. random environment.
Acta Mathematica Scientia,
Vol. 32,
Issue. 3,
p.
1193.
Gao, Zhenlong
and
Zhang, Yanhua
2014.
A Weak Limit Theorem for Galton-Watson Processes in Varying Environments.
Journal of Applied Mathematics,
Vol. 2014,
Issue. ,
p.
1.
Li, Yingqiu
Liu, Quansheng
Gao, Zhiqiang
and
Wang, Hesong
2014.
Asymptotic properties of supercritical branching processes in random environments.
Frontiers of Mathematics in China,
Vol. 9,
Issue. 4,
p.
737.
Gao, Zhenlong
and
Zhang, Yanhua
2015.
Limit Theorems for a Galton–Watson Process with Immigration in Varying Environments.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 38,
Issue. 4,
p.
1551.
Iksanov, Alexander
and
Kabluchko, Zakhar
2016.
A central limit theorem and a law of the iterated logarithm for the Biggins martingale of the supercritical branching random walk.
Journal of Applied Probability,
Vol. 53,
Issue. 4,
p.
1178.
Comets, Francis
and
Liu, Quansheng
2017.
Rate of convergence for polymers in a weak disorder.
Journal of Mathematical Analysis and Applications,
Vol. 455,
Issue. 1,
p.
312.
Maillard, Pascal
and
Pain, Michel
2019.
1-stable fluctuations in branching Brownian motion at critical temperature I: The derivative martingale.
The Annals of Probability,
Vol. 47,
Issue. 5,
Ren, Yan-Xia
Song, Renming
Sun, Zhenyao
and
Zhao, Jianjie
2019.
Stable central limit theorems for super Ornstein-Uhlenbeck processes.
Electronic Journal of Probability,
Vol. 24,
Issue. none,
Iksanov, Alexander
Kolesko, Konrad
and
Meiners, Matthias
2020.
Fluctuations of Biggins’ martingales at complex parameters.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 56,
Issue. 4,
Cosco, Clément
and
Nakajima, Shuta
2021.
Gaussian fluctuations for the directed polymer partition function in dimension d≥3 and in the whole L2-region.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 57,
Issue. 2,
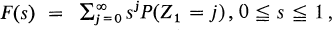 where 1 < m = EZ 1 < ∞. The Galton-Watson process evolves in such a way that the generating function Fn (s) of Zn is the nth functional iterate of F(s). The convergence problem for Z n, when appropriately normed, has been studied by quite a number of authors; for an ultimate form see Heyde [2]. However, no information has previously been obtained on the rate of such convergence. We shall here suppose that
where 1 < m = EZ 1 < ∞. The Galton-Watson process evolves in such a way that the generating function Fn (s) of Zn is the nth functional iterate of F(s). The convergence problem for Z n, when appropriately normed, has been studied by quite a number of authors; for an ultimate form see Heyde [2]. However, no information has previously been obtained on the rate of such convergence. We shall here suppose that 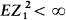 in which case Wn = m –nZn converges almost surely to a non-degenerate random variable W as n → ∞ (Harris [1], p. 13). It is our object to establish the following result on the rate of convergence of Wn to W.
in which case Wn = m –nZn converges almost surely to a non-degenerate random variable W as n → ∞ (Harris [1], p. 13). It is our object to establish the following result on the rate of convergence of Wn to W.
