Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Papastavridis, S.
1987.
A limit theorem for the reliability of a consecutive-k-out-of-n system.
Advances in Applied Probability,
Vol. 19,
Issue. 3,
p.
746.
Papastavridis, Stavros G.
1988.
A weibull limit for the reliability of a consecutivek-within-m-out-of-nsystem.
Advances in Applied Probability,
Vol. 20,
Issue. 3,
p.
690.
Papastavridis, Stavros G.
1988.
A weibull limit for the reliability of a consecutivek-within-m-out-of-nsystem.
Advances in Applied Probability,
Vol. 20,
Issue. 3,
p.
690.
Papastavridis, S.
and
Hadzichristos, I.
1988.
Formulas for the reliability of a consecutive-K-Out-of-n: F system.
Journal of Applied Probability,
Vol. 25,
Issue. 04,
p.
772.
Boland, Philip J.
Proschan, Frank
and
Tong, Y. L.
1989.
Optimal arrangement of components via pairwise rearrangements.
Naval Research Logistics,
Vol. 36,
Issue. 6,
p.
807.
Papastavridis, S.
1989.
The number of failed components in a consecutive-k-of-n:F system.
IEEE Transactions on Reliability,
Vol. 38,
Issue. 3,
p.
338.
Chao, M. T.
and
Fu, James C.
1989.
A limit theorem of certain repairable systems.
Annals of the Institute of Statistical Mathematics,
Vol. 41,
Issue. 4,
p.
809.
Papastavridis, S.G.
1989.
Lifetime distribution of circular consecutive-k-out-of-n:F systems with exchangeable lifetimes.
IEEE Transactions on Reliability,
Vol. 38,
Issue. 4,
p.
460.
Hwang, F.K.
1989.
Invariant permutations for consecutive k-out-of-n cycles.
IEEE Transactions on Reliability,
Vol. 38,
Issue. 1,
p.
65.
Kuo, W.
Zhang, W.
and
Zuo, M.
1990.
A consecutive-k-out-of-n:G system: the mirror image of a consecutive-k-out-of-n:F system.
IEEE Transactions on Reliability,
Vol. 39,
Issue. 2,
p.
244.
Papastavridis, S.
1990.
m-consecutive-k-out-of-n:F systems.
IEEE Transactions on Reliability,
Vol. 39,
Issue. 3,
p.
386.
Schilling, Mark F.
1990.
The Longest Run of Heads.
The College Mathematics Journal,
Vol. 21,
Issue. 3,
p.
196.
Boland, Philip J.
Proschan, Frank
and
Tong, Y. L.
1990.
Linear Dependence in Consecutive k-out-of-n: F Systems.
Probability in the Engineering and Informational Sciences,
Vol. 4,
Issue. 3,
p.
391.
Chryssaphinou, Ourania
and
Papastavridis, Stavros
1990.
Reliability of a consecutive-k-out-of-n system in a random environment.
Journal of Applied Probability,
Vol. 27,
Issue. 02,
p.
452.
Lau, Tai Shing
1992.
The reliability of exchangeable binary systems.
Statistics & Probability Letters,
Vol. 13,
Issue. 2,
p.
153.
Sfakianakis, M.
Kounias, S.
and
Hillaris, A.
1992.
Reliability of a consecutive k-out-of-r-from-n:F system.
IEEE Transactions on Reliability,
Vol. 41,
Issue. 3,
p.
442.
Sfakianakis, M.E.
and
Papastavridis, S.G.
1993.
Reliability of a general consecutive-k-out-of-n:F system.
IEEE Transactions on Reliability,
Vol. 42,
Issue. 3,
p.
491.
Koutras, Markos V.
and
Papastavridis, Stavros G.
1993.
Application of the stein-chen method for bounds and limit theorems in the reliability of coherent structures.
Naval Research Logistics,
Vol. 40,
Issue. 5,
p.
617.
Boland, Philip J.
1993.
Reliability and Decision Making.
p.
287.
Papastavridis, Stavros G.
and
Koutras, Markos V.
1993.
New Trends in System Reliability Evaluation.
Vol. 16,
Issue. ,
p.
228.

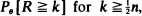 and a rearrangement inequality. The inequality is applied to solve an optimal permutation problem for consecutive-
and a rearrangement inequality. The inequality is applied to solve an optimal permutation problem for consecutive-