Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T09:41:41.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Scale-free percolation in continuous space: quenched degree and clustering coefficient

Part of: Graph theory

Published online by Cambridge University Press:  25 February 2021

Joseba Dalmau  and
Michele Salvi Open the ORCID record for Michele Salvi [Opens in a new window]
Joseba Dalmau*
Affiliation:
NYU Shanghai
Michele Salvi*
Affiliation:
LPSM, Université de Paris
*
*Postal address: Institute of Mathematical Sciences, NYU Shanghai, Geography Building, 3663 North Zhongshan Road, Shanghai, China.
**Postal address: Laboratoire de Probabilités, Statistique et Modélisation (LPSM), Université de Paris – Sorbonne Université – CNRS, 1 place Aurélie Nemours, 75013 Paris, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

Spatial random graphs capture several important properties of real-world networks. We prove quenched results for the continuous-space version of scale-free percolation introduced in [14]. This is an undirected inhomogeneous random graph whose vertices are given by a Poisson point process in 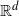$\mathbb{R}^d$. Each vertex is equipped with a random weight, and the probability that two vertices are connected by an edge depends on their weights and on their distance. Under suitable conditions on the parameters of the model, we show that, for almost all realizations of the point process, the degree distributions of all the nodes of the graph follow a power law with the same tail at infinity. We also show that the averaged clustering coefficient of the graph is self-averaging. In particular, it is almost surely equal to the annealed clustering coefficient of one point, which is a strictly positive quantity.

Keywords

Random graphscale-free percolationdegree distributionclustering coefficientsmall worldPoisson point processself-averaging

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C63: Infinite graphs 05C82: Small world graphs, complex networks 05C90: Applications
Type
Research Papers
Information
Journal of Applied Probability , Volume 58 , Issue 1 , March 2021 , pp. 106 - 127
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albert, R., Jeong, H. and Barabási, A.-L. (1999). Internet: diameter of the world-wide web. Nature 401, 130.CrossRefGoogle Scholar
Barabási, A.-L. and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.CrossRefGoogle ScholarPubMed
Barrat, A. and Weigt, M. (2000). On the properties of small-world network models. Eur. Phys. J. B 13, 547–560.CrossRefGoogle Scholar
Barthélemy, M. (2011). Spatial networks. Phys. Rep. 499, 1–101.CrossRefGoogle Scholar
Berger, N. (2002). Transience, recurrence and critical behavior for long-range percolation. Commun. Math. Phys. 226, 531–558.CrossRefGoogle Scholar
Biskup, M. (2004). On the scaling of the chemical distance in long-range percolation models. Ann. Prob. 32, 2938–2977.CrossRefGoogle Scholar
Bringmann, K., Keusch, R. and Lengler, J. (2019). Geometric inhomogeneous random graphs. Theoret. Comput. Sci. 760, 35–54.CrossRefGoogle Scholar
Candellero, E. and Fountoulakis, N. (2016). Clustering and the hyperbolic geometry of complex networks. Internet Math. 12, 2–53.CrossRefGoogle Scholar
Chung, F. and Lu, L. (2002). The average distances in random graphs with given expected degrees. Proc. Nat. Acad. Sci. USA 99, 15879–15882.CrossRefGoogle Scholar
Cont, R., Moussa, A. and Bastos e Santos, E. (2010). Network structure and systemic risk in banking systems. SSRN Electron. J. http://dx.doi.org/10.2139/ssrn.1733528.CrossRefGoogle Scholar
Coupechoux, E. and Lelarge, M. (2014). How clustering affects epidemics in random networks. Adv. Appl. Prob. 46, 985–1008.CrossRefGoogle Scholar
Daley, D. J. and Vere-Jones, D. (2008). An Introduction to the Theory of Point Processes, vol. II: General Theory and Structure, 2nd edn (Probability and its Applications). Springer, New York.CrossRefGoogle Scholar
Deijfen, M., van der Hofstad, R. and Hooghiemstra, G. (2013). Scale-free percolation. Ann. Inst. H. Poincaré Prob. Statist. 49, 817–838.CrossRefGoogle Scholar
Deprez, P. and Wüthrich, M. V. (2019). Scale-free percolation in continuum space. Commun. Math. Statist. 7, 269–308.CrossRefGoogle Scholar
Deprez, P., Hazra, R. S. and Wüthrich, M. V. (2015). Inhomogeneous long-range percolation for real-life network modeling. Risks 3, 1–23.CrossRefGoogle Scholar
Dutta, B. L., Ezanno, P. and Vergu, E. (2014). Characteristics of the spatio-temporal network of cattle movements in France over a 5-year period. Preventive Veterinary Medicine 117, 79–94.CrossRefGoogle ScholarPubMed
Feller, W. (1971). An Introduction to Probability Theory and its Applications, vol. 2, 2nd edn. John Wiley, New York.Google Scholar
Fountoulakis, N., van der Hoorn, P., Müller, T. and Schepers, M. (2020). Clustering in a hyperbolic model of complex networks. Available at arXiv:2003.05525.Google Scholar
Gracar, P., Grauer, A., Lüchtrath, L. and Mörters, P. (2019). The age-dependent random connection model. Queueing Systems 93, 309–331.CrossRefGoogle Scholar
Gugelmann, L., Panagiotou, K. and Peter, U. (2012). Random hyperbolic graphs: degree sequence and clustering. In International Colloquium on Automata, Languages, and Programming (Lecture Notes Comput. Sci. 7392), pp. 573–585. Springer.CrossRefGoogle Scholar
Haenggi, M., Andrews, J. G., Baccelli, F., Dousse, O. and Franceschetti, M. (2009). Stochastic geometry and random graphs for the analysis and design of wireless networks. IEEE J. Sel. Areas Commun. 27, 1029–1046.CrossRefGoogle Scholar
Heydenreich, M., Hulshof, T. and Jorritsma, J. (2017). Structures in supercritical scale-free percolation. Ann. Appl. Prob. 27, 2569–2604.CrossRefGoogle Scholar
Jacob, E. and Mörters, P. (2015). Spatial preferential attachment networks: power laws and clustering coefficients. Ann. Appl. Prob. 25, 632–662.CrossRefGoogle Scholar
Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N. and Barabási, A.-L. (2000). The large-scale organization of metabolic networks. Nature 407, 651.CrossRefGoogle ScholarPubMed
Kaluza, P., Kölzsch, A., Gastner, M. T. and Blasius, B. (2010). The complex network of global cargo ship movements. J. R. Soc. Interface 7, 1093–1103.CrossRefGoogle ScholarPubMed
Kingman, J. F. C. (1992). Poisson Processes, vol. 3. Clarendon Press.Google Scholar
Komjáthy, J. and Lodewijks, B. (2020). Explosion in weighted hyperbolic random graphs and geometric inhomogeneous random graphs. Stochastic Process. Appl. 130, 1309–1367.CrossRefGoogle Scholar
Lago-Fernández, L. F., Huerta, R., Corbacho, F. and Sigüenza, J. A. (2000). Fast response and temporal coherent oscillations in small-world networks. Phys. Rev. Lett. 84, 2758.CrossRefGoogle ScholarPubMed
Mitzenmacher, M. and Upfal, E. (2017). Probability and Computing: Randomization and Probabilistic Techniques in Algorithms and Data Analysis. Cambridge University Press.Google Scholar
Moller, J. and Waagepetersen, R. P. (2003). Statistical Inference and Simulation for Spatial Point Processes. Chapman & Hall/CRC.CrossRefGoogle Scholar
Moore, C. and Newman, M. E. (2000). Epidemics and percolation in small-world networks. Phys. Rev. E 61, 5678.CrossRefGoogle ScholarPubMed
Newman, M. E. (2003). The structure and function of complex networks. SIAM Rev. 45, 167–256.CrossRefGoogle Scholar
Newman, M. E., Watts, D. J. and Strogatz, S. H. (2002). Random graph models of social networks. Proc. Nat. Acad. Sci. USA 99, 2566–2572.CrossRefGoogle Scholar
Norros, I. and Reittu, H. (2006). On a conditionally Poissonian graph process. Adv. Appl. Prob. 38, 59–75.CrossRefGoogle Scholar
Pastor-Satorras, R. and Vespignani, A. (2001). Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200.CrossRefGoogle ScholarPubMed
Riley, S., Eames, K., Isham, V., Mollison, D. and Trapman, P. (2015). Five challenges for spatial epidemic models. Epidemics 10, 68–71.CrossRefGoogle ScholarPubMed
Soramäki, K., Bech, M. L., Arnold, J., Glass, R. J. and Beyeler, W. E. (2007). The topology of interbank payment flows. Physica A 379, 317–333.CrossRefGoogle Scholar
Stegehuis, C., van Der Hofstad, R. and van Leeuwaarden, J. S. (2019). Scale-free network clustering in hyperbolic and other random graphs. J. Phys. A 52, 295101.CrossRefGoogle Scholar
Van Der Hofstad, R. (2016). Random Graphs and Complex Networks, vol. 1. Cambridge University Press.Google Scholar
Watts, D. J. and Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440.CrossRefGoogle ScholarPubMed
Yukich, J. (2006). Ultra-small scale-free geometric networks. J. Appl. Prob. 43, 665–677.CrossRefGoogle Scholar