Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T09:44:17.126Z Has data issue: false hasContentIssue false
  • English
  • Français

Sequential metric dimension for random graphs

Part of: Discrete mathematics in relation to computer science Combinatorial probability Graph theory

Published online by Cambridge University Press:  22 November 2021

Gergely Ódor Open the ORCID record for Gergely Ódor [Opens in a new window]  and
Patrick Thiran
Gergely Ódor*
Affiliation:
EPFL
Patrick Thiran*
Affiliation:
EPFL
*
*Postal address: IINFCOM INDY2, École Polytechnique Fédérale de Lausanne, EPFL-IC Station 14 - Bâtiment BC, CH-1015 Lausanne, Switzerland
*Postal address: IINFCOM INDY2, École Polytechnique Fédérale de Lausanne, EPFL-IC Station 14 - Bâtiment BC, CH-1015 Lausanne, Switzerland
Get access Rights & Permissions [Opens in a new window]

Abstract

In the localization game on a graph, the goal is to find a fixed but unknown target node 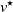$v^\star$ with the least number of distance queries possible. In the jth step of the game, the player queries a single node 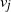$v_j$ and receives, as an answer to their query, the distance between the nodes 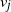$v_j$ and 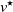$v^\star$ . The sequential metric dimension (SMD) is the minimal number of queries that the player needs to guess the target with absolute certainty, no matter where the target is.

The term SMD originates from the related notion of metric dimension (MD), which can be defined the same way as the SMD except that the player’s queries are non-adaptive. In this work we extend the results of Bollobás, Mitsche, and Prałat [4] on the MD of Erdős–Rényi graphs to the SMD. We find that, in connected Erdős–Rényi graphs, the MD and the SMD are a constant factor apart. For the lower bound we present a clean analysis by combining tools developed for the MD and a novel coupling argument. For the upper bound we show that a strategy that greedily minimizes the number of candidate targets in each step uses asymptotically optimal queries in Erdős–Rényi graphs. Connections with source localization, binary search on graphs, and the birthday problem are discussed.

Keywords

Source detectionbinary search on graphsexpansion properties of Erdős–Rényi graphs

MSC classification

Primary: 05C80: Random graphs
Secondary: 68R05: Combinatorics 05C85: Graph algorithms 60C05: Combinatorial probability
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 4 , December 2021 , pp. 909 - 951
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arratia, R. and DeSalvo, S. (2013). On the singularity of random Bernoulli matrices: novel integer partitions and lower bound expansions. Ann. Combin. 17, 251–274.CrossRefGoogle Scholar
Arratia, R., Goldstein, L. and Gordon, L. (1989). Two moments suffice for Poisson approximations: the Chen–Stein method. Ann. Prob. 17, 9–25.10.1214/aop/1176991491CrossRefGoogle Scholar
Bensmail, J., Mazauric, D., Mc Inerney, F., Nisse, N. and Pérennes, S. (2018). Sequential metric dimension. In 16th International Workshop on Approximation and Online Algorithms, pp. 36–50. Springer.CrossRefGoogle Scholar
Bollobás, B., Mitsche, D. and Prałat, P. (2013). Metric dimension for random graphs. Electron. J. Combin. 20, P1.10.37236/2639CrossRefGoogle Scholar
Cáceres, J., Hernando, C., Mora, M., Pelayo, I. M., Puertas, M. L., Seara, C. and Wood, D. R. (2007). On the metric dimension of cartesian products of graphs. SIAM J. Discrete Math. 21, 423–441.CrossRefGoogle Scholar
Dudek, A., English, S., Frieze, A., MacRury, C. and Prałat, P. (2019). Localization game for random graphs. Available at arXiv:1910.11225.Google Scholar
Dudek, A., Frieze, A. and Pegden, W. (2019). A note on the localization number of random graphs: diameter two case. Discrete Appl. Math. 254, 107–112.10.1016/j.dam.2018.06.006CrossRefGoogle Scholar
Emamjomeh-Zadeh, E., Kempe, D. and Singhal, V. (2016). Deterministic and probabilistic binary search in graphs. In Proceedings of the Forty-Eighth Annual ACM Symposium on Theory of Computing, pp. 519–532. ACM.10.1145/2897518.2897656CrossRefGoogle Scholar
Frieze, A., Martin, R., Moncel, J., Ruszinkó, M. and Smyth, C. (2007). Codes identifying sets of vertices in random networks. Discrete Math. 307, 1094–1107.10.1016/j.disc.2006.07.041CrossRefGoogle Scholar
Harary, F. and Melter, R. A. (1976). On the metric dimension of a graph. Ars Combin. 2, 191–195.Google Scholar
Janson, S. (1998). New versions of Suen’s correlation inequality. Random Struct. Algorithms 13, 467–483.3.0.CO;2-W>CrossRefGoogle Scholar
Kahn, J., Komlós, J. and Szemerédi, E. (1995). On the probability that a random $\pm 1$ -matrix is singular. J. Amer. Math. Soc. 8, 223–240.Google Scholar
Karpovsky, M. G., Chakrabarty, K. and Levitin, L. B. (1998). On a new class of codes for identifying vertices in graphs. IEEE Trans. Inf. Theory 44, 599–611.10.1109/18.661507CrossRefGoogle Scholar
Kim, Y., Kumbhat, M., Nagy, Z. L., Patkós, B., Pokrovskiy, A. and Vizer, M. (2015). Identifying codes and searching with balls in graphs. Discrete Appl. Math. 193, 39–47.CrossRefGoogle Scholar
Komlós, J. (1967). On the determinant of (0, 1) matrices. Studia Sci. Math. Hung. 2, 7–,21.Google Scholar
Lecomte, V., Ódor, G. and Thiran, P. (2020). Noisy source location on a line. Available at arXiv:2002.07336.Google Scholar
Mase, S. (1992). Approximations to the birthday problem with unequal occurrence probabilities and their application to the surname problem in Japan. Ann. Inst. Statist. Math. 44, 479–499.Google Scholar
Mitsche, D. and Rué, J. (2015). On the limiting distribution of the metric dimension for random forests. Europ. J. Combinatorics 49, 68–89.10.1016/j.ejc.2015.02.029CrossRefGoogle Scholar
Nowak, R. D. (2011). The geometry of generalized binary search. IEEE Trans. Inf. Theory 57, 7893–7906.CrossRefGoogle Scholar
Ódor, G. odorgergo/dynamic_source_localization_toolbox: First release July 2020.Google Scholar
Pinto, P. C., Thiran, P. and Vetterli, M. (2012). Locating the source of diffusion in large-scale networks. Phys. Rev. Lett. 109, 068702.10.1103/PhysRevLett.109.068702CrossRefGoogle ScholarPubMed
Seager, S. M. (2013). A sequential locating game on graphs. Ars Combin. 110, 45–54.Google Scholar
Shah, D. and Zaman, T. (2011). Rumors in a network: Who’s the culprit? IEEE Trans. Inf. Theory 57, 5163–5181.10.1109/TIT.2011.2158885CrossRefGoogle Scholar
Slater, P. J. (1975). Leaves of trees. Congr. Numer. 14, 549–559.Google Scholar
Spinelli, B., Celis, L. E. and Thiran, P. (2016). Observer placement for source localization: the effect of budgets and transmission variance. In 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), pp. 743–751. IEEE.10.1109/ALLERTON.2016.7852307CrossRefGoogle Scholar
Spinelli, B., Celis, L. E. and Thiran, P. (2018). How many sensors to localize the source? The double metric dimension of random networks. In 2018 56th Annual Allerton Conference on Communication, Control, and Computing (Allerton), pp. 1036–1043. IEEE.10.1109/ALLERTON.2018.8635897CrossRefGoogle Scholar
Spinelli, B., Celis, L. E. and Thiran, P. (2019). A general framework for sensor placement in source localization. IEEE Trans. Network Sci. Eng. 6, 86–102.CrossRefGoogle Scholar
Suen, W. S. (1990). A correlation inequality and a Poisson limit theorem for nonoverlapping balanced subgraphs of a random graph. Random Structures Algorithms 1, 231–242.CrossRefGoogle Scholar
Tao, T. and Vu, V. (2006). On random $\pm 1$ matrices: singularity and determinant. Random Structures Algorithms 28, 1–23.CrossRefGoogle ScholarPubMed
Zejnilović, S., Gomes, J. and Sinopoli, B. (2013). Network observability and localization of the source of diffusion based on a subset of nodes. In 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), pp. 847–852. IEEE.CrossRefGoogle Scholar
Zejnilović, S., Gomes, J. and Sinopoli, B. (2015). Sequential observer selection for source localization. In 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), pp. 1220–1224. IEEE.10.1109/GlobalSIP.2015.7418392CrossRefGoogle Scholar