Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barbour, Andrew D.
and
Schuh, H.-J.
1979.
Functional normalizations for the branching process with infinite mean.
Journal of Applied Probability,
Vol. 16,
Issue. 03,
p.
513.
Schuh, H.-J.
1979.
Some results on the structure of irregular branching processes by infinite mean.
Advances in Applied Probability,
Vol. 11,
Issue. 02,
p.
292.
Vatutin, V. A.
and
Zubkov, A. M.
1987.
Branching processes. I.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 1,
p.
2431.
van der Hofstad, Remco
Hooghiemstra, Gerard
and
Znamenski, Dmitri
2007.
Distances in Random Graphs with Finite Mean and Infinite Variance Degrees.
Electronic Journal of Probability,
Vol. 12,
Issue. none,
van der Hofstad, Remco
and
Hooghiemstra, Gerard
2008.
Universality for distances in power-law random graphs.
Journal of Mathematical Physics,
Vol. 49,
Issue. 12,
2010.
Introduction to Stochastic Models.
p.
343.
Athreya, K. B.
and
Hong, Jyy-I
2013.
An Application of the Coalescence Theory to Branching Random Walks.
Journal of Applied Probability,
Vol. 50,
Issue. 03,
p.
893.
Baroni, Enrico
van der Hofstad, Remco
and
Komjáthy, Júlia
2017.
Nonuniversality of weighted random graphs with infinite variance degree.
Journal of Applied Probability,
Vol. 54,
Issue. 1,
p.
146.
Adriaans, Erwin
and
Komjáthy, Júlia
2018.
Weighted Distances in Scale-Free Configuration Models.
Journal of Statistical Physics,
Vol. 173,
Issue. 3-4,
p.
1082.
Bhattacharya, Ayan
and
Palmowski, Zbigniew
2019.
Slower variation of the generation sizes induced by heavy-tailed environment for geometric branching.
Statistics & Probability Letters,
Vol. 154,
Issue. ,
p.
108550.
Baroni, Enrico
van der Hofstad, Remco
and
Komjáthy, Júlia
2019.
Tight Fluctuations of Weight-Distances in Random Graphs with Infinite-Variance Degrees.
Journal of Statistical Physics,
Vol. 174,
Issue. 4,
p.
906.
Komjáthy, Júlia
and
Lodewijks, Bas
2020.
Explosion in weighted hyperbolic random graphs and geometric inhomogeneous random graphs.
Stochastic Processes and their Applications,
Vol. 130,
Issue. 3,
p.
1309.
Park, Su-Chan
Krug, Joachim
Touzo, Léo
and
Mörters, Peter
2023.
Branching with Selection and Mutation I: Mutant Fitness of Fréchet Type.
Journal of Statistical Physics,
Vol. 190,
Issue. 7,
Ray, Souvik
Hazra, Rajat Subhra
Roy, Parthanil
and
Soulier, Philippe
2023.
Branching random walk with infinite progeny mean: A tale of two tails.
Stochastic Processes and their Applications,
Vol. 160,
Issue. ,
p.
120.


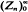 denote the simple branching process with
denote the simple branching process with 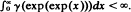 Then lim
Then lim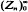 process.
process.