Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T09:28:59.710Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple conditions for metastability of continuous Markov chains

Part of: Markov processes Probabilistic methods, simulation and stochastic differential equations

Published online by Cambridge University Press:  25 February 2021

Oren Mangoubi ,
Natesh Pillai  and
Aaron Smith
Oren Mangoubi*
Affiliation:
Worcester Polytechnic Institute
Natesh Pillai*
Affiliation:
Harvard University
Aaron Smith*
Affiliation:
University of Ottawa
*
*Postal address: Worcester Polytechnic Institute, 100 Institute Road, Worcester, Massachusetts, USA. Email address: omangoubi@gmail.com
**Postal address: Department of Statistics, Harvard University, 1 Oxford Street, Cambridge, MA 02138, USA.
***Postal address: Department of Mathematics and Statistics, University of Ottawa, 585 King Edward Avenue, Ottawa ON K1N 7N5, Canada.
Get access Rights & Permissions [Opens in a new window]

Abstract

A family 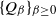$\{Q_{\beta}\}_{\beta \geq 0}$ of Markov chains is said to exhibit metastable mixing with modes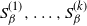$S_{\beta}^{(1)},\ldots,S_{\beta}^{(k)}$ if its spectral gap (or some other mixing property) is very close to the worst conductance 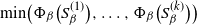$\min\!\big(\Phi_{\beta}\big(S_{\beta}^{(1)}\big), \ldots, \Phi_{\beta}\big(S_{\beta}^{(k)}\big)\big)$ of its modes for all large values of 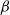$\beta$. We give simple sufficient conditions for a family of Markov chains to exhibit metastability in this sense, and verify that these conditions hold for a prototypical Metropolis–Hastings chain targeting a mixture distribution. The existing metastability literature is large, and our present work is aimed at filling the following small gap: finding sufficient conditions for metastability that are easy to verify for typical examples from statistics using well-studied methods, while at the same time giving an asymptotically exact formula for the spectral gap (rather than a bound that can be very far from sharp). Our bounds from this paper are used in a companion paper (O. Mangoubi, N. S. Pillai, and A. Smith, arXiv:1808.03230) to compare the mixing times of the Hamiltonian Monte Carlo algorithm and a random walk algorithm for multimodal target distributions.

Keywords

MetastabilityMarkov chain Monte Carlo (MCMC)spectral gapmultimodal distribution

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces
Secondary: 65C40: Computational Markov chains
Type
Research Papers
Information
Journal of Applied Probability , Volume 58 , Issue 1 , March 2021 , pp. 83 - 105
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beltrán, J. and Landim, C. (2015). A martingale approach to metastability. Prob. Theory Relat. Fields 161, 267–307.CrossRefGoogle Scholar
Bovier, A. and Den Hollander, F. (2006). Metastability: A Potential Theoretic Approach. Springer, New York.Google Scholar
Cheeger, J. (1970). A lower bound for the smallest eigenvalue of the Laplacian. In Problems in Analysis, ed. Gunning, R. C., Princeton University Press, pp. 195–199.Google Scholar
Griffeath, D. (1975). A maximal coupling for Markov chains. Z. Wahrscheinlichkeitsth. 31, 95–106.CrossRefGoogle Scholar
Jerrum, M., Son, J.-B., Tetali, P. and Vigoda, E. (2004). Elementary bounds on Poincaré and log-Sobolev constants for decomposable Markov chains. Ann. Appl. Prob. 14, 1741–1765.CrossRefGoogle Scholar
Landim, C. (2018). Metastable Markov chains. Preprint.Google Scholar
Lawler, G. F. and Sokal, A. D. (1988). Bounds on the $L^2$ spectrum for Markov chains and Markov processes: a generalization of Cheeger’s inequality. Trans. Am. Math. Soc. 309, 557–580.Google Scholar
Levin, D. A., Peres, Y. and Wilmer, E. L. (2009). Markov Chains and Mixing Times. American Mathematical Society, Providence, RI.Google Scholar
Lovász, J. and Vempala, S. (2006). Hit-and-run from a corner. SIAM J. Comp. 35, 985–1005.CrossRefGoogle Scholar
Madras, N. and Randall, D. (2002). Markov chain decomposition for convergence rate analysis. Ann. Appl. Prob. 12, 581–606.Google Scholar
Mangoubi, O., Pillai, N. S. and Smith, A. (2018). Does Hamiltonian Monte Carlo mix faster than a random walk on multimodal densities? Preprint. arXiv:1808.03230.Google Scholar
Mangoubi, O. and Smith, A. (2017). Mixing of Hamiltonian Monte Carlo on strongly log-concave distributions 1: Continuous dynamics. Preprint.Google Scholar
Mangoubi, O. and Smith, A. (2017). Rapid mixing of Hamiltonian Monte Carlo on strongly log-concave distributions. Preprint. arXiv:1708.07114.Google Scholar
Mengersen, K. L. and Tweedie, R. L. (1996). Rates of convergence of the Hastings and Metropolis algorithms. Ann. Statist. 24, 101–121.Google Scholar
Meyn, S. P. and Tweedie, R. L. (1994). Computable bounds for geometric convergence rates of Markov chains. Ann. Appl. Prob. 4, 981–1011.CrossRefGoogle Scholar
Olivieri, E. and Vares, M. E. (2005). Large Deviations and Metastability. Cambridge University Press.CrossRefGoogle Scholar
Pillai, N. S. and Smith, A. (2017). Elementary bounds on mixing times for decomposable Markov chains. Stoch. Process. Appl. 127, 3068–3109.CrossRefGoogle Scholar
Resnick, S. I. (2013). A Probability Path. Springer, New York.Google Scholar
Roberts, G. O., Gelman, A. and Gilks, W. R. (1997). Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann. Appl. Prob. 7, 110–120.Google Scholar
Roberts, G. O. and Rosenthal, J. S. (1997). Geometric ergodicity and hybrid Markov chains. Electron. Commun. Prob. 2, 13–25.CrossRefGoogle Scholar
Rosenthal, J. S. (1995). Minorization conditions and convergence rates for Markov chain Monte Carlo. J. Am. Statist. Assoc. 90, 558–566.CrossRefGoogle Scholar
Turchin, V. F. (1971). On the computation of multidimensional integrals by the Monte-Carlo method. Theory Prob. Appl. 16, 720–724.CrossRefGoogle Scholar
Woodard, D., Schmidler, S. and Huber, M. (2009). Sufficient conditions for torpid mixing of parallel and simulated tempering. Electron. J. Prob. 14, 780–804.CrossRefGoogle Scholar
Woodard, D. B., Schmidler, S. C. and Huber, M. (2009). Conditions for rapid mixing of parallel and simulated tempering on multimodal distributions. Ann. Appl. Prob. 19, 617–640.CrossRefGoogle Scholar