Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-11T11:57:18.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Some characterizations of exponential or geometric distributions in a non-stationary record value model

Part of: Distribution theory Singular integral equations Distribution theory - Probability

Published online by Cambridge University Press:  14 July 2016

Hans-Jürgen Witte
Hans-Jürgen Witte*
Affiliation:
University of Oldenburg
*
∗ Postal address: Carl von Ossietzky Universität Oldenburg, Fachbereich 6 Mathematik, Postfach 2503, DW-2900 Oldenburg, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let {Fn}n ≧ 0 be a sequence of c.d.f. and let {Rn}n ≧ 1 be the sequence of record values in a non-stationary record model where after the (n − 1)th record the population is distributed according to Fn. Then the equidistribution of the nth population and the record increment Rn – Rn– 1 (i.e. Rn – Rn– 1~ Fn) characterizes Fn to have an exponentially decreasing hazard function. To be more precise Fn is the exponential distribution if the support of Rn– 1 generates a dense subgroup in 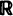and otherwise the entity of all possible solutions can be obtained in the following way: let for simplicity the above additive subgroup be 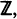any c.d.f. F satisfying F(0) = 0, F(1) < 1 can be chosen arbitrarily. Setting λ = – log(1 – F(1)), Fn(x) = 1 – F(x – [x])exp(–λ [x]) 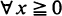is an admissible solution coinciding with F on the interval [0, 1] ([x] denotes the integer part of x). Simple additional assumptions ensuring that Fn is either exponential or geometric are given. Similar results for exponential or geometric tail distributions based on the independence of Rn– 1 and Rn – Rn– 1 are proved.

Keywords

EXPONENTIAL TAIL DISTRIBUTIONSGEOMETRIC (TAIL) DISTRIBUTIONSRECORD VALUES IN A NON-STATIONARY MODELORDER STATISTICSINTEGRATED CAUCHY FUNCTIONAL EQUATIONCHARACTERIZATION PROBLEMS

MSC classification

Primary: 60E05: Distributions
Secondary: 62E10: Characterization and structure theory 45E10: Integral equations of the convolution type (Abel, Picard, Toeplitz and Wiener-Hopf type)
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 2 , June 1993 , pp. 373 - 381
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahsannullah, M. (1978a) Record values and the exponential distribution. Ann. Inst. Statist. Math. 30, 429–433.CrossRefGoogle Scholar
Ahsanullah, M. (1978b) A characterization of the exponential distribution by spacings. J. Appl. Prob. 15, 650–653.CrossRefGoogle Scholar
Ahsanullah, M. (1979) Characterization of the exponential distribution by record values. Sankhya B 41, 116–121.Google Scholar
Ahsanullah, M. and Holland, B. (1987) Distributional properties of record values from the geometrical distribution. Statist. Neerl. 41, 129–137.CrossRefGoogle Scholar
Choquet, D. and Deny, J. (1960) Sur l'equation de convolution µ = µ* s. C. R. Acad. Sci. Paris 250, 799–801.Google Scholar
Deheuvels, P. (1984) The characterization of distributions by order statistics and record values – a unified approach. J. Appl. Prob. 21, 326–334.Google Scholar
Gupta, R. C. (1984) Relationships between order statistics and record values and some characterization results. J. Appl. Prob. 21, 425–430.CrossRefGoogle Scholar
Lau, K. and Rao, C. R. (1982) Integrated Cauchy functional equation and characterization of the exponential law. Sankhya A 44, 72–90.Google Scholar
Lau, K. and Rao, C. R. (1984) Solution to the integrated Cauchy functional equation on the whole line. Sankhya A 46, 311–318.Google Scholar
Nagaraja, H. N. (1988) Record values and related statistics – a review. Comm. Statist. – Theory Meth. A 17, 2223–2238.CrossRefGoogle Scholar
Nagaraja, H. N., Sen, P. and Srivastava, R. C. (1990) Some characterizations of geometric tail distributions based on record values. Stat. Papers. To appear.CrossRefGoogle Scholar
Nayak, S. S. (1981) Characterizations based on record values. J. Indian Statist. Assoc. 19, 123–127.Google Scholar
Nevzorov, V. B. (1986) Two characterizations using records. In Stability Problems for Stochastic Models. Lecture Notes in Mathematics 1233, 79-85. Springer-Verlag, Berlin.Google Scholar
Nevzorov, V. B. (1988) Records. Theory Prob. Appl. 32, 201–228.CrossRefGoogle Scholar
Pfeifer, D. (1980) Record values in einem stochastischen Modell mit nicht-identischen Verteilungen. , RWTH Aachen.Google Scholar
Pfeifer, D. (1982) Characterizations of exponential distributions by independent nonstationary record increments. J. Appl. Prob. 19, 127–135 (Correction 19, 906).CrossRefGoogle Scholar
Pfeifer, D. (1991) Some remarks on Nevzorov's record model. Adv. Appl. Prob. 23, 823–834.CrossRefGoogle Scholar
Ramachandran, B. (1982) On the equation f (x) = ?(0,8) f (x + y) dµ (y) . Sankhya A 44, 364–371.Google Scholar
Ramachandran, B. (1984) Renewal type equations on ℤ. Sankhya A 46, 319–325.Google Scholar
Ramchandran, B. and Rao, B. L. S. P. (1984) On the equation f (x) = ?8-8 f (x + y) dµ (y) . Sankhya A 46, 326–338.Google Scholar
Rao, C. R. (1983) An extension of Deny's theory and its application to characterization of probability distributions. In A Festschrift for Eric Lehmann, ed. Bickel, P. J. et al., pp. 348–365, Wadsworth, Monterey, CA.Google Scholar
Rao, C. R. and Shanbhag, D. N. (1986) Recent results on characterization of probability distributions: a unified approach through extensions of Deny's theorem. Adv. Appl. Prob. 18, 660–678.Google Scholar
Shanbhag, D. N. (1977) An extension of the Rao-Rubin characterization of the Poisson distribution. J. Appl. Prob. 14, 640–646.CrossRefGoogle Scholar
Srivastava, R. C. (1979) Two characterizations of the geometric distribution by record values. Sankhya B 40, 276–278.Google Scholar
Srivastava, R. C. (1981) On some characterization of the geometrical distribution. In Statistical Distributions in Scientific Work, Vol. 4, ed. Taillie, C., Batil, G. P. and Baldessari, B. A., pp. 349–356, Reidel, Dordrecht.CrossRefGoogle Scholar
Tata, M. N. (1969) On outstanding values in a sequence of random variables. Z. Wahrscheinlichkeitsth. 12, 9–20.CrossRefGoogle Scholar
Witte, H.-J. (1988) Some characterizations of distributions based on the integrated Cauchy functional equation. Sankhya A 50, 59–63.Google Scholar
Witte, H.-J. (1990) Characterizations of distributions of exponential or geometric type by the integrated lack of memory property and record values. Comp. Stat. Dat. Anal. 10, 283–288.CrossRefGoogle Scholar
Zijlstra, M. (1983) Characterizations of the geometric distribution by distributional properties. J. Appl. Prob. 20, 843–850.Google Scholar