Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T06:25:22.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Some effects of trimming on the law of the iterated logarithm

Part of: Nonparametric inference Limit theorems

Published online by Cambridge University Press:  14 July 2016

Harry Kesten  and
Ross Maller
Harry Kesten
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853-7901, USA. Email address: kesten@math.comell.edu
Ross Maller
Affiliation:
Department of Accounting and Finance, University of Western Australia, Nedlands, WA 6097, Australia. Email address: ross.maller@anu.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate some effects that the ‘light' trimming of a sum Sn = X1 + X2 + · ·· + Xn of independent and identically distributed random variables has on behaviour of iterated logarithm type. Light trimming is defined as removing a constant number of summands from Sn. We consider two versions: (r)Sn, which is obtained by deleting the r largest Xi from Sn, and 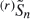, which is obtained by deleting the r variables Xi which are largest in absolute value from Sn. We summarise some relevant results from Rogozin (1968), Heyde (1969), and later writers concerning the untrimmed sum, and add some new results concerning trimmed sums. Among other things we show that a general form of the law of the iterated logarithm holds for 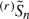but not (completely) for .

Keywords

trimmed sumorder statisticsiterated logarithm law

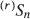MSC classification

Primary: 60F15: Strong theorems
Secondary: 60F05: Central limit and other weak theorems 62G30: Order statistics; empirical distribution functions
Type
Part 5. Properties of random variables
Information
Journal of Applied Probability , Volume 41 , Issue A: Stochastic Methods and their Applications , 2004 , pp. 253 - 271
Copyright
Copyright © Applied Probability Trust 2004 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bingham, N. (1986). Variants on the law of the iterated logarithm. Bull. London Math. Soc. 18, 433–467.CrossRefGoogle Scholar
Gnedenko, B. V. and Kolmogorov, A. N. (1954). Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Cambridge, MA.Google Scholar
Hartman, P. and Wintner, A. (1941). On the law of the iterated logarithm. Amer. J. Math. 63, 169–176.CrossRefGoogle Scholar
Heyde, C. C. (1968). On the converse to the iterated logarithm law. J. Appl. Prob. 5, 210–215.CrossRefGoogle Scholar
Heyde, C. C. (1969). A note concerning behaviour of iterated logarithm type. Proc. Amer. Math. Soc. 23, 85–90.CrossRefGoogle Scholar
Heyde, C. C. (1982). Law of the iterated logarithm. In Encyclopedia of Statistical Sciences , Vol 4, eds Kotz, S., Johnson, N. L. and Read, C. B., John Wiley, New York, pp. 528–530.Google Scholar
Kesten, H. (1972). Sums of independent random variables–without moment conditions. Ann. Math. Statist. 43. 701–732.CrossRefGoogle Scholar
Kesten, H. and Maller, R. A. (1992). Ratios of trimmed sums and order statistics. Ann. Prob. 20, 1805–1842.CrossRefGoogle Scholar
Kesten, H. and Maller, R. A. (1994). Infinite limits and infinite limit points of random walks and trimmed sums. Ann. Prob. 22, 1473–1513.CrossRefGoogle Scholar
Kesten, H. and Maller, R. A. (1995). The effect of trimming on the strong law of large numbers. Proc. London Math. Soc. 71, 441–480.CrossRefGoogle Scholar
Klass, M. J. (1976). Toward a universal law of the iterated logarithm. I. Z. Wahrscheinlichkeitsth. 36, 165–178.CrossRefGoogle Scholar
Klass, M. J. (1977). Toward a universal law of the iterated logarithm. II. Z. Wahrscheinlichkeitsth. 39, 151–165.CrossRefGoogle Scholar
Kuelbs, J. and Zinn, J. (1983). Some results of LIL behavior. Ann. Prob. 11, 506–557.CrossRefGoogle Scholar
Lévy, P. (1937). Théorie de l'Addition des Variables Aléatoires. Gauthier-Villars, Paris.Google Scholar
Maller, R. A. (1980a). A note on domains of partial attraction. Ann. Prob. 8, 576–583.CrossRefGoogle Scholar
Maller, R. A. (1980b). On one-sided boundedness of normed partial sums. Bull. Austral. Math. Soc. 21, 373–391.CrossRefGoogle Scholar
Maller, R. A. (1988). A functional law of the iterated logarithm for distributions in the domain of partial attraction of the normal distribution. Stoch. Process. Appl. 27, 179–194.CrossRefGoogle Scholar
Martikainen, A. I. (1980). A criterion for strong relative stability of random walk on the line. Mat. Zametki 28, 619–622.Google Scholar
Mori, T. (1976). The strong law of large numbers when extreme terms are removed from sums. Z. Wahrscheinlichkeitsth. 36, 189–193.CrossRefGoogle Scholar
Petrov, V. V. (1995). Law of the iterated logarithm. In Encyclopedia of Mathematics , Vol. 5 (translated from the Russian), ed. Hazewinkel, M., Kluwer, Dordrecht, pp. 373–374.Google Scholar
Pruitt, W. E. (1981). General one-sided laws of the iterated logarithm. Ann. Prob. 9, 1–48.CrossRefGoogle Scholar
Rogozin, B. A. (1968). On the existence of exact upper sequences. Theory Prob. Appl. 13, 667–672.CrossRefGoogle Scholar
Rosalsky, A. (1981). On the growth of a random walk centered at a median. Sankya A 43, 111–115.Google Scholar
Strassen, V. (1964). An invariance principle for the law of the iterated logarithm. Z Wahrscheinlichkeitsth. 3, 211–226.CrossRefGoogle Scholar
Strassen, V. (1965). A converse to the law of the iterated logarithm. Z. Wahrscheinlichkeitsth. 4, 265–268.CrossRefGoogle Scholar