Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T21:20:47.265Z Has data issue: false hasContentIssue false
  • English
  • Français

The spitzer identity for some bivariate processes in queueing theory: an algebraic approach

Published online by Cambridge University Press:  24 August 2016

Gerd Schmidt
Gerd Schmidt*
Affiliation:
Universität des Saarlandes
*
∗Postal address: Fachbereich Angewandte Mathematik und Informatik, Universität des Saarlandes, 6600 Saarbrücken, FRG.
Get access Rights & Permissions [Opens in a new window]

Abstract

This note deals with a purely algebraic development of the Spitzer identity for a bivariate Markov process 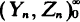, which is important for random walks, dams and queues. This identity, comprising the results of Kingman on the process 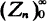, has been known for a long time in an analytic form as a solution of a certain integral equation. The algebraic approach leads to explicit results of interesting structure. In particular, the bivariate distribution of (Yn, Zn) can be expressed in terms of the marginal distributions of the stochastically dependent variables Yn and Zn.

Keywords

RANDOM WALKSQUEUEING THEORYSTORAGE
Type
Research Paper
Information
Journal of Applied Probability , Volume 23 , Issue 4 , December 1986 , pp. 1000 - 1007
Copyright
Copyright © Applied Probability Trust 1986 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Cohen, J. W. (1969) The Single Server Queue. North-Holland, Amsterdam.Google Scholar
[2] Kingman, J. F. C. (1966) On the algebra of queues. J. Appl. Prob. 3, 285–326.Google Scholar
[3] Pollaczek, F. (1957) Problèmes Stochastiques Posés par le Phénomène de Formation d'une Queue d'attente à un Guichet et par des Phénomènes Apparantes. Gauthiers Villars, Paris.Google Scholar