Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T08:17:08.244Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic comparisons of random processes, with applications in reliability

Published online by Cambridge University Press:  14 July 2016

Gordon Pledger  and
Frank Proschan
Gordon Pledger*
Affiliation:
The Florida State University
Frank Proschan
Affiliation:
The Florida State University
*
*Now at the University of Texas at Austin.
Get access Rights & Permissions [Opens in a new window]

Abstract

The usual definition of stochastic comparison of random vectors is extended to stochastic comparison of random processes. Conditions are stated under which {X (t), t ≧ 0} stochastically larger than {Y (t), t ≧ 0} implies that 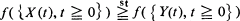for increasing functionals f.

Applications are made to reliability problems, yielding stochastic comparisons for systems of independently operating machines assuming exponential failure and exponential repair. From these stochastic comparisons we may then deduce similar stochastic comparisons for functionals of practical importance in reliability applications, such as the total machine up-time, the first time that the number of functioning machines drops below a specified number, the total time during which at least a specified number of machines are functioning, etc.

Keywords

STOCHASTIC COMPARISONRANDOM PROCESSESRELIABILITYPROPORTIONAL HAZARDSALTERNATING FAILURE AND REPAIR
Type
Research Papers
Information
Journal of Applied Probability , Volume 10 , Issue 3 , September 1973 , pp. 572 - 585
Copyright
Copyright © Applied Probability Trust 1973 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research sponsored by the Air Force Office of Scientific Research, AFSC, USAF, under Grant no AFORS-71-2058 and the National Science Foundation under Grant no. GU 2612.

References

Barlow, R. E. and Proschan, F. (1965) Mathematical Theory of Reliability. John Wiley, New York.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. John Wiley, New York.Google Scholar
Esary, J. D., Marshall, A. W. and Proschan, F. (1970) Some reliability applications of the hazard transform. SIAM J. Appl. Math. 18, 849–860.Google Scholar
Mitrinovic, D. S. (1971) Analytic Inequalities. Springer-Verlag, Berlin.Google Scholar
Pledger, G. and Proschan, F. (1971) Comparisons of order statistics and of spacings from heterogeneous distributions. In Optimizing Methods in Statistics. Ed. Rustagi, J. S. Academic Press, New York.Google Scholar
Veinott, A. F. Jr. (1965) Optimal policy in a dynamic, single product, nonstationary inventory model with several demand classes. Operations Research 13, 761–778.10.1287/opre.13.5.761Google Scholar