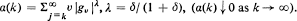Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MATSUMOTO, Tadahiko
and
ARIYOSHI, Michiyasu
1975.
Nishi Nihon Hifuka,
Vol. 37,
Issue. 2,
p.
258.
Chanda, Kamal C.
1976.
Some comments on sample quantiles for dependent observations.
Communications in Statistics - Theory and Methods,
Vol. 5,
Issue. 14,
p.
1385.
Gorodetskii, V. V.
1978.
On the Strong Mixing Property for Linear Sequences.
Theory of Probability & Its Applications,
Vol. 22,
Issue. 2,
p.
411.
Chanda, Kamal C.
and
Kulp, Richard W.
1978.
On some nonparametric estimators for the linear markov scheme.
Communications in Statistics - Theory and Methods,
Vol. 7,
Issue. 5,
p.
427.
1980.
Statistical Inference for Stochastic Processes.
p.
415.
Chanda, Kamal C.
1981.
Statistical Distributions in Scientific Work.
p.
35.
Withers, C. S.
1981.
Conditions for linear processes to be strong-mixing.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 57,
Issue. 4,
p.
477.
Andrews, Donald W. K.
1984.
Non-strong mixing autoregressive processes.
Journal of Applied Probability,
Vol. 21,
Issue. 04,
p.
930.
Andrews, Donald W. K.
1985.
A Zero-One Result for the Least Squares Estimator.
Econometric Theory,
Vol. 1,
Issue. 1,
p.
85.
Pham, Tuan D.
and
Tran, Lanh T.
1985.
Some mixing properties of time series models.
Stochastic Processes and their Applications,
Vol. 19,
Issue. 2,
p.
297.
Athreya, Krishna B.
and
Pantula, Sastry G.
1986.
A note on strong mixing of ARMA processes.
Statistics & Probability Letters,
Vol. 4,
Issue. 4,
p.
187.
Athreya, Krishna B.
and
Pantula, Sastry G.
1986.
Mixing properties of harris chains and autoregressive processes.
Journal of Applied Probability,
Vol. 23,
Issue. 4,
p.
880.
Athreya, Krishna B.
and
Pantula, Sastry G.
1986.
Mixing properties of harris chains and autoregressive processes.
Journal of Applied Probability,
Vol. 23,
Issue. 04,
p.
880.
Roussas, George G.
and
Ioannides, D.
1987.
Moment inequalities for mixing sequences of random variables.
Stochastic Analysis and Applications,
Vol. 5,
Issue. 1,
p.
60.
Tran, L.T.
1989.
Recursive density estimation under dependence.
IEEE Transactions on Information Theory,
Vol. 35,
Issue. 5,
p.
1103.
Chanda, K. C.
and
Ruymgaart, F. H.
1990.
GENERAL LINEAR PROCESSES:A PROPERTY OF THE EMPIRICAL PROCESS APPLIED TO DENSITY AND MODE ESTIMATION.
Journal of Time Series Analysis,
Vol. 11,
Issue. 3,
p.
185.
Pötscher, Benedikt M.
and
Prucha, Ingmar R.
1991.
Basic structure of the asymptotic theory in dynamic nonlineaerco nometric models, part i: consistency and approximation concepts.
Econometric Reviews,
Vol. 10,
Issue. 2,
p.
125.
Härdle, Wolfgang
and
Vieu, Philippe
1992.
KERNEL REGRESSION SMOOTHING OF TIME SERIES.
Journal of Time Series Analysis,
Vol. 13,
Issue. 3,
p.
209.
F de Lima, Pedro J.
1996.
Nuisance parameter free properties of correlation integral based statistics.
Econometric Reviews,
Vol. 15,
Issue. 3,
p.
237.
Yu, Jun
1997.
Uniform convergence rates for a nearest neighbor density estimator under dependence assumptions.
Communications in Statistics - Theory and Methods,
Vol. 26,
Issue. 3,
p.
601.

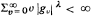 where
where 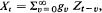 , where the identity is to be understood in the sense of convergence in distribution. Then {
, where the identity is to be understood in the sense of convergence in distribution. Then {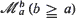 is the
is the 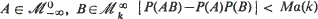 where
where