Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kaplan, Norman
and
Pakes, A.G.
1974.
Supercritical age-dependent branching processes with immigration.
Stochastic Processes and their Applications,
Vol. 2,
Issue. 4,
p.
371.
Grey, D. R.
1976.
On possible rates of growth of age-dependent branching processes with immigration.
Journal of Applied Probability,
Vol. 13,
Issue. 01,
p.
138.
Parthasarathy, P.R.
and
Krishnamoorthy, A.
1977.
Compounding Bellman-Harris processes allowing immigration.
Mathematical Biosciences,
Vol. 37,
Issue. 1-2,
p.
105.
Vatutin, V. A.
and
Zubkov, A. M.
1987.
Branching processes. I.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 1,
p.
2431.
Rahimov, I.
1995.
Branching Processes.
Vol. 99,
Issue. ,
p.
58.
Butkovsky, O. A.
2012.
Limit behavior of a critical branching process with immigration.
Mathematical Notes,
Vol. 92,
Issue. 5-6,
p.
612.
Бутковский, Олег Александрович
and
Butkovskij, Oleg Aleksandrovich
2012.
Предельное поведение критического ветвящегося процесса с иммиграцией.
Математические заметки,
Vol. 92,
Issue. 5,
p.
670.
SUN, HONGWEI
and
WU, QIANG
2013.
INDEFINITE KERNEL NETWORK WITH DEPENDENT SAMPLING.
Analysis and Applications,
Vol. 11,
Issue. 05,
p.
1350020.
Zhang, Meijian
and
Sun, Hongwei
2017.
Regression learning with non-identically and non-independently sampling.
International Journal of Wavelets, Multiresolution and Information Processing,
Vol. 15,
Issue. 01,
p.
1750007.

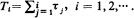 . These particles evolve according to a one-dimensional age-dependent branching process with offspring p.g.f.
. These particles evolve according to a one-dimensional age-dependent branching process with offspring p.g.f. 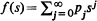 and life time distribution
and life time distribution 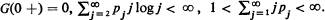 . Then it is shown that
. Then it is shown that 