Article contents
Sur la Lp convergence des martingales liées au recouvrement
Published online by Cambridge University Press: 14 July 2016
Abstract
In a coverage problem introduced by Dvoretzky (1956) the circle is covered with lengths 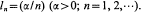 The associated indexed martingale can be considered as a set of random densities with respect to Lebesgue measure, of which the limit is a random measure. The total masses of the set constitute a new martingale. From a theorem of Shepp (1972), this martingale does not converge in a space
The associated indexed martingale can be considered as a set of random densities with respect to Lebesgue measure, of which the limit is a random measure. The total masses of the set constitute a new martingale. From a theorem of Shepp (1972), this martingale does not converge in a space 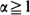 if
if 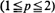 . If 0 < α < 1 it converges in all spaces
. If 0 < α < 1 it converges in all spaces 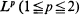 , and in this paper we demonstrate that it converges in all spaces Lp for p > 2. We also obtain quite precise estimates for the moments of the total mass of the limit measure, showing that the characteristic function of this total mass is an entire function of order 1/(1 − α). Thus in some sense the mass is distributed in a bounded domain.
, and in this paper we demonstrate that it converges in all spaces Lp for p > 2. We also obtain quite precise estimates for the moments of the total mass of the limit measure, showing that the characteristic function of this total mass is an entire function of order 1/(1 − α). Thus in some sense the mass is distributed in a bounded domain.
MSC classification
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1995
References
Références
- 3
- Cited by


