No CrossRef data available.
Article contents
Time-convergent random matrices from mean-field pinned interacting eigenvalues
Published online by Cambridge University Press: 18 November 2022
Abstract
We study a multivariate system over a finite lifespan represented by a Hermitian-valued random matrix process whose eigenvalues (i) interact in a mean-field way and (ii) converge to their weighted ensemble average at their terminal time. We prove that such a system is guaranteed to converge in time to the identity matrix that is scaled by a Gaussian random variable whose variance is inversely proportional to the dimension of the matrix. As the size of the system grows asymptotically, the eigenvalues tend to mutually independent diffusions that converge to zero at their terminal time, a Brownian bridge being the archetypal example. Unlike commonly studied random matrices that have non-colliding eigenvalues, the proposed eigenvalues of the given system here may collide. We provide the dynamics of the eigenvalue gap matrix, which is a random skew-symmetric matrix that converges in time to the 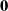 $\textbf{0}$ matrix. Our framework can be applied in producing mean-field interacting counterparts of stochastic quantum reduction models for which the convergence points are determined with respect to the average state of the entire composite system.
$\textbf{0}$ matrix. Our framework can be applied in producing mean-field interacting counterparts of stochastic quantum reduction models for which the convergence points are determined with respect to the average state of the entire composite system.
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust


