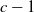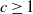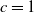Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schilling, Judith
2021.
Results and conjectures on the role of the uniform distribution in the coupon collector's problem with group drawings.
Information Processing Letters,
Vol. 169,
Issue. ,
p.
106112.
Chenavier, Nicolas
Henze, Norbert
and
Otto, Moritz
2022.
Limit laws for large th-nearest neighbor balls.
Journal of Applied Probability,
Vol. 59,
Issue. 3,
p.
880.
Betken, Carina
and
Thäle, Christoph
2023.
Approaching the coupon collector’s problem with group drawings via Stein’s method.
Journal of Applied Probability,
Vol. 60,
Issue. 4,
p.
1352.
Mladenović, Pavle
2024.
Extreme Values In Random Sequences.
p.
189.
Henze, Norbert
2024.
Asymptotic Stochastics.
Vol. 10,
Issue. ,
p.
35.
Athreya, Siva
Mukherjee, Satyaki
and
Mukherjee, Soumendu Sundar
2025.
On a Generalisation of the Coupon Collector Problem.
Journal of Theoretical Probability,
Vol. 38,
Issue. 3,