Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Iglehart, Donald L.
and
Whitt, Ward
1970.
Multiple channel queues in heavy traffic. II: sequences, networks, and batches.
Advances in Applied Probability,
Vol. 2,
Issue. 2,
p.
355.
Hooke, John A.
1970.
On some limit theorems for the GI/G/1 queue.
Journal of Applied Probability,
Vol. 7,
Issue. 03,
p.
634.
Whitt, Ward
1971.
Weak convergence theorems for priority queues: preemptive-resume discipline.
Journal of Applied Probability,
Vol. 8,
Issue. 01,
p.
74.
Serfozo, Richard F.
1972.
Processes with conditional stationary independent increments.
Journal of Applied Probability,
Vol. 9,
Issue. 02,
p.
303.
Whitt, Ward
1972.
Stochastic Abelian and Tauberian theorems.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 22,
Issue. 4,
p.
251.
Serfozo, Richard F.
1972.
Processes with conditional stationary independent increments.
Journal of Applied Probability,
Vol. 9,
Issue. 2,
p.
303.
Kennedy, Douglas P.
1972.
Rates of convergence for queues in heavy traffic. I.
Advances in Applied Probability,
Vol. 4,
Issue. 2,
p.
357.
Whitt, Ward
1974.
Mathematical Methods in Queueing Theory.
Vol. 98,
Issue. ,
p.
307.
Serfozo, Richard F.
1975.
Functional limit theorems for stochastic processes based on embedded processes.
Advances in Applied Probability,
Vol. 7,
Issue. 01,
p.
123.
Serfozo, Richard F.
1975.
Functional limit theorems for stochastic processes based on embedded processes.
Advances in Applied Probability,
Vol. 7,
Issue. 1,
p.
123.
Parthasarathy, P.R.
and
Krishnamoorthy, A.
1977.
Compounding Bellman-Harris processes allowing immigration.
Mathematical Biosciences,
Vol. 37,
Issue. 1-2,
p.
105.
Vervaat, Wim
1979.
On a stochastic difference equation and a representation of non–negative infinitely divisible random variables.
Advances in Applied Probability,
Vol. 11,
Issue. 04,
p.
750.
1979.
Correction.
Advances in Applied Probability,
Vol. 11,
Issue. 4,
p.
889.
1979.
Correction.
Advances in Applied Probability,
Vol. 11,
Issue. 04,
p.
889.
Tautu, P.
1980.
Modelle in der Medizin.
Vol. 22,
Issue. ,
p.
304.
Glynn, P. W.
and
Whitt, W.
1986.
A central-limit-theorem version ofL=?w.
Queueing Systems,
Vol. 1,
Issue. 2,
p.
191.
Pang, G.
Kesidis, G.
and
Konstantopoulos, T.
2012.
Avoiding overages by deferred aggregate demand for PEV charging on the smart grid.
p.
3322.
Iksanov, Alexander
Marynych, Alexander
and
Meiners, Matthias
2017.
Asymptotics of random processes with immigration I: Scaling limits.
Bernoulli,
Vol. 23,
Issue. 2,

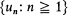 be a sequence of non-negative random variables and
be a sequence of non-negative random variables and 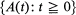 the associated point process defined by
the associated point process defined by