Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T02:42:50.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Zipf’s law for atlas models

Part of: Stochastic analysis Mathematical economics Mathematical sociology Mathematical finance

Published online by Cambridge University Press:  23 November 2020

Ricardo T. Fernholz  and
Robert Fernholz
Ricardo T. Fernholz*
Affiliation:
Claremont McKenna College
Robert Fernholz*
Affiliation:
Intech Investment Management, LLC
*
*Postal address: 500 E. Ninth St., Claremont, CA 91711, USA. Email address: rfernholz@cmc.edu
**Postal address: One Palmer Square, Princeton, NJ 08542, USA. Email address: bob@bobfernholz.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A set of data with positive values follows a Pareto distribution if the log–log plot of value versus rank is approximately a straight line. A Pareto distribution satisfies Zipf’s law if the log–log plot has a slope of 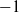$-1$. Since many types of ranked data follow Zipf’s law, it is considered a form of universality. We propose a mathematical explanation for this phenomenon based on Atlas models and first-order models, systems of strictly positive continuous semimartingales with parameters that depend only on rank. We show that the stationary distribution of an Atlas model will follow Zipf’s law if and only if two natural conditions, conservation and completeness, are satisfied. Since Atlas models and first-order models can be constructed to approximate systems of time-dependent rank-based data, our results can explain the universality of Zipf’s law for such systems. However, ranked data generated by other means may follow non-Zipfian Pareto distributions. Hence, our results explain why Zipf’s law holds for word frequency, firm size, household wealth, and city size, while it does not hold for earthquake magnitude, cumulative book sales, and the intensity of wars, all of which follow non-Zipfian Pareto distributions.

Keywords

Zipf’s lawPareto distributionAtlas modelfirst-order model

MSC classification

Primary: 60H30: Applications of stochastic analysis (to PDE, etc.)
Secondary: 91B70: Stochastic models 91G70: Statistical methods, econometrics 91D20: Mathematical geography and demography
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 4 , December 2020 , pp. 1276 - 1297
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atkinson, A. B., Piketty, T. and Saez, E. (2011). Top incomes in the long run of history. J. Econom. Lit. 49, 3–71.10.1257/jel.49.1.3CrossRefGoogle Scholar
Axtell, R. (2001). Zipf distribution of U.S. firm sizes. Science 293, 1818–1820.10.1126/science.1062081CrossRefGoogle ScholarPubMed
Bak, P. (1996). How Nature Works. Springer, New York.10.1007/978-1-4757-5426-1CrossRefGoogle Scholar
Banner, A., Fernholz, R. and Karatzas, I. (2005). On Atlas models of equity markets. Ann. Appl. Prob. 15, 2296–2330.10.1214/105051605000000449CrossRefGoogle Scholar
Banner, A. and Ghomrasni, R. (2008). Local times of ranked continuous semimartingales. Stoch. Process Appl. 118, 1244–1253.10.1016/j.spa.2007.08.001CrossRefGoogle Scholar
Bass, R. and Pardoux, E. (1987). Uniqueness for diffusions with piecewise constant coefficients. Prob. Theory Relat. Fields 76, 557–572.10.1007/BF00960074CrossRefGoogle Scholar
Blanchet, T., Fournier, J. and Piketty, T. (2017). Generalized Pareto curves: theory and applications. Technical report. World Wealth & Income Database.Google Scholar
Brown, R. (1827). Brownian motion. Unpublished experiment.Google Scholar
Bruggeman, C. (2016). Dynamics of large rank-based systems of interacting diffusions. PhD thesis, Columbia University.Google Scholar
Chatterjee, S. and Pal, S. (2010). A phase transition behavior for Brownian motions interacting through their ranks. Prob. Theory Relat. Fields 147, 123–159.10.1007/s00440-009-0203-0CrossRefGoogle Scholar
Dembo, A., Jara, M. and Olla, S. (2017). The infinite Atlas process: convergence to equilibrium. Ann. Inst. H. Poincaré Prob. Statist. 55, 607–619.10.1214/17-AIHP875CrossRefGoogle Scholar
Dembo, A., Shkolnikov, M., Varadhan, S. R. S. and Zeitouni, O. (2016). Large deviations for diffusions interacting through their ranks. Commun. Pure Appl. Math. 69, 1259–1313.10.1002/cpa.21640CrossRefGoogle Scholar
Dembo, A. and Tsai, L.-C. (2017). Equilibrium fluctuation of the Atlas model. Ann. Prob. 45, 4529–4560.10.1214/16-AOP1171CrossRefGoogle Scholar
Fernholz, E. R. (2002). Stochastic Portfolio Theory. Springer, New York.10.1007/978-1-4757-3699-1CrossRefGoogle Scholar
Fernholz, R., Ichiba, T. and Karatzas, I. (2013). A second-order stock market model. Ann. Finance 9, 1–16.10.1007/s10436-012-0193-2CrossRefGoogle Scholar
Fernholz, R., Ichiba, T. and Karatzas, I. (2013). Two Brownian particles with rank-based characteristics and skew-elastic collisions. Stoch. Process. Appl. 123, 2999–3026.10.1016/j.spa.2013.03.019CrossRefGoogle Scholar
Fernholz, R., Ichiba, T., Karatzas, I. and Prokaj, V. (2013). A planar diffusion with rank-based characteristics and perturbed Tanaka equations. Prob. Theory Relat. Fields 156, 343–374.10.1007/s00440-012-0430-7CrossRefGoogle Scholar
Fernholz, R. and Karatzas, I. (2009). Stochastic portfolio theory: an overview. In Mathematical Modelling and Numerical Methods in Finance: Special Volume, Handbook of Numerical Analysis, eds A. Bensoussan and Q. Zhang, Vol. XV. North-Holland, Amsterdam, pp. 89–168.Google Scholar
Fernholz, R. T. and Koch, C. (2016). Why are big banks getting bigger? Working Paper 1604. Federal Reserve Bank of Dallas.Google Scholar
Fernholz, R. T. and Koch, C. (2017). Big banks, idiosyncratic volatility, and systemic risk. Amer. Econom. Rev. 107, 603–607.10.1257/aer.p20171007CrossRefGoogle Scholar
Gabaix, X. (1999). Zipf’s law for cities: an explanation. Quart. J. Econom. 114, 739–767.10.1162/003355399556133CrossRefGoogle Scholar
Gabaix, X. (2009). Power laws in economics and finance. Ann. Rev. Econom. 1, 255–294.10.1146/annurev.economics.050708.142940CrossRefGoogle Scholar
Harrison, J. and Reiman, M. (1981). Reflected Brownian motion on an orthant. Ann. Prob. 9, 302–308.10.1214/aop/1176994471CrossRefGoogle Scholar
Harrison, J. M. and Williams, R. J. (1987). Brownian models of open queueing networks with homogeneous customer populations. Stochastics 22, 77–115.10.1080/17442508708833469CrossRefGoogle Scholar
Harrison, J. M. and Williams, R. J. (1987). Multidimensional reflected Brownian motions having exponential stationary distributions. Ann. Prob. 15, 115–137.10.1214/aop/1176992259CrossRefGoogle Scholar
Ichiba, T. and Karatzas, I. (2010). On collisions of Brownian particles. Ann. Appl. Prob. 20, 951–977.10.1214/09-AAP641CrossRefGoogle Scholar
Ichiba, T., Karatzas, I. and Shkolnikov, M. (2013). Strong solutions of stochastic equations with rank-based coefficients. Prob. Theory Relat. Fields 156, 229–248.10.1007/s00440-012-0426-3CrossRefGoogle Scholar
Ichiba, T., Pal, S. and Shkolnikov, M. (2013). Convergence rates for rank-based models with applications to portfolio theory. Prob. Theory Relat. Fields 156, 415–448.10.1007/s00440-012-0432-5CrossRefGoogle Scholar
Ichiba, T., Papathanakos, V., Banner, A., Karatzas, I. and Fernholz, R. (2011). Hybrid Atlas models. Ann. Appl. Prob. 21, 609–644.10.1214/10-AAP706CrossRefGoogle Scholar
Karatzas, I. and Shreve, S. E. (1991). Brownian Motion and Stochastic Calculus. Springer, New York.Google Scholar
Khas’minskii, R. Z. (1960). Ergodic properties of recurrent diffusion processes, and stabilization of the solution to the Cauchy problem for parabolic equations. Theory Prob. Appl. 5, 179–196.10.1137/1105016CrossRefGoogle Scholar
Khas’minskii, R. Z. (1980). Stochastic Stability of Differential Equations. Sijthoff and Noordhoff, Amsterdam.10.1007/978-94-009-9121-7CrossRefGoogle Scholar
Neumark, D., Wall, B. and Zhang, J. (2011). Do small businesses create more jobs? New evidence for the United States from the National Establishment Time Series. Rev. Econom. Statist. 93, 16–29.10.1162/REST_a_00060CrossRefGoogle Scholar
Newman, M. E. J. (2005). Power laws, Pareto distributions, and Zipf’s law. Contemp. Phys. 46, 323–351.10.1080/00107510500052444CrossRefGoogle Scholar
Pal, S. and Pitman, J. (2008). One-dimensional Brownian particle systems with rank-dependent drifts. Ann. Appl. Prob. 18, 2179–2207.10.1214/08-AAP516CrossRefGoogle Scholar
Sarantsev, A. (2015). Triple and simultaneous collisions of competing Brownian particles. Electron. J. Prob. 20, 1–28.10.1214/EJP.v20-3279CrossRefGoogle Scholar
Simon, H. and Bonini, C. (1958). The size distribution of business firms. Amer. Econom. Rev. 48, 607–617.Google Scholar
Simon, H. A. (1955). On a class of skew distribution functions. Biometrika 42, 425–440.10.1093/biomet/42.3-4.425CrossRefGoogle Scholar
Soo, K. T. (2005). Zipf’s law for cities: a cross-country investigation. Regional Sci. Urban Econom. 35, 239–263.10.1016/j.regsciurbeco.2004.04.004CrossRefGoogle Scholar
Stroock, D. W. and Varadhan, S. R. S. (2006). Multidimensional Diffusion Processes. Springer, Berlin.Google Scholar
Tao, T. (2012). E pluribus unum: from complexity, universality. Daedalus 141, 23–34.10.1162/DAED_a_00158CrossRefGoogle Scholar
Wikipedia (2020). Zipf’s law. https://en.wikipedia.org/wiki/Zipf%27s_law.Google Scholar
Williams, R. J. (1987). Reflected Brownian motion with skew symmetric data in a polyhedral domain. Prob. Theory Relat. Fields 75, 459–485.10.1007/BF00320328CrossRefGoogle Scholar
Zipf, G.(1935). The Psychology of Language: An Introduction to Dynamic Philology. MIT Press, Cambridge, MA.Google Scholar