Let {Xt}t≧0 (t may be discrete or continuous) be a random process whose finite-dimensional distributions are of exponential type. The first-passage time inf{t:Xt≧f(t)}, where f(t) is a positive, continuous function, such that f(t)= o(t) as t↑∞, is considered. The problem of finiteness of its moments is solved for both the case that {Xt}t≧0 has stationary independent increments as well as the case in which no assumptions are made about stationarity and independence for the increments of the process. Applications to sequential estimation are also given.

Suppose Y is the strength of a system subjected to a sequence of stresses X1, X2, X3, · ··. Let N(t) be the number of stresses occurring by time t and let T be the lifetime of the system. Then the survival distribution of is given by where and . In this note we aim at determining from the above model various non-parametric classes of life distributions which are of interest in reliability theory.

A series of bounds for the availability and unavailability in a fixed time interval, I, for a system of maintained, interdependent components are given in Natvig (1980) in the traditional binary case, and in Funnemark and Natvig (1985) in the multistate case. For the special case of independent components the only assumption needed to arrive at these bounds is that the marginal performance process of each component is associated in I. When these processes are Markovian and binary, a sufficient condition for this to hold is given by Esary and Proschan (1970). In the present paper we generalize this condition to the multistate case, and give an equivalent and much more convenient condition in terms of the transition intensities.

We consider the problem of minimizing the long-run average cost per unit time of operating a finite dam in the class of the policies 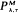of the following type. Assume that the dam is initially empty, the release rate is kept at 0 until the dam storage increases to λ, and as soon as this occurs, water is released at rate M, then the output rate is kept at M as long as the dam storage is more than τ and it must be decreased to 0 if the dam storage becomes τ. We assume that the input of water into the finite dam is a Wiener process with non-negative drift μ and variance parameter σ2. There is a cost in increasing the output rate from 0 to M as well as in decreasing the rate from M to 0 and whenever the dam storage is below level a, there is a penalty cost per unit time depending on the level. A reward is given for each unit of water released. In this paper, the long-run average cost per unit time is determined, and therefore the optimal policy 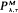can be found numerically.