Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T13:43:32.718Z Has data issue: false hasContentIssue false
  • English
  • Français

A Linear-Programming Approach to Evaluating Restrictions Under a Bond Indenture or Loan Agreement

Published online by Cambridge University Press:  19 October 2009

James Van Horne
Get access Rights & Permissions [Opens in a new window]

Extract

When a company enters into a bond indenture or loan agreement, certain restrictions usually are placed on it. These restrictions, known as protective covenants, may have a significant influence on profitability, making the bargaining strategy of the company very important. But to bargain effectively over the restrictiveness of the protective covenants, management must know the impact that the covenants have on profitability.

Type
Research Article
Information
Journal of Financial and Quantitative Analysis , Volume 1 , Issue 2 , June 1966 , pp. 68 - 83
Copyright
Copyright © School of Business Administration, University of Washington 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Other applications of mathematical programming to financial management decision making include Charnes, A., Cooper, W. W., and Miller, M. H., “Application of Linear Programming to Financial Budgeting and the Costing of Funds,” Journal of Business, XXXII (January 1959), pp. 20–46Google Scholar; Ijiri, Y., Levy, F. K. and Lyon, R. C., “A Linear Programming Model for Budgeting and Financial Planning,” Journal of Accounting Research, I (Autumn 1963), pp. 198–212Google Scholar; Robichek, A. A., Teichroew, D. and Jones, J. M., “Optimal Short Term Financing Decision,” Management Science, XII (September 1965), pp. 1–36Google Scholar; and Weingartner, H. Martin, Mathematical Programming and the Analysis of Capital Budgeting Decisions (Englewood Cliffs, N.J.: Prentice-Hall, Inc., 1963).Google Scholar

2 As a matter of terminology, a lender will be interpreted as being either a bondholder, whose interests are administered by a trustee, or a direct lender, such as a bank or an insurance company. Similarly, a loan will be considered to be either the purchase of bonds by investors or a direct loan.

3 See Jacoby, N. H. and Saulnier, R. J., Term Lending to Business (Camden, N. J.: National Bureau of Economic Research, 1942), p. 76Google Scholar; and Robinson, Roland I., The Management of Bank Funds (New York: McGraw- Hill Book Company, Inc., 1962), pp. 253–256.Google Scholar

4 It is assumed that until some terminal date, net cash benefits generated from an investment proposal are reinvested at the company's existing cost of capital. See Hirshleifer, J., “On the Theory of Optimal Investment,” Journal of Political Economy, LXVI (August 1958), pp. 329–352Google Scholar; Lorie, J. H. and Savage, L. J., “Three Problems in Rationing Capital,” Journal of Business XXVIII (October 1955), pp. 229–239Google Scholar; and Solomon, Ezra, The Theory of Financial Management (New York: Columbia University Press, 1963), pp. 132–135.Google Scholar

5 Lindsay, Robert and Sametz, Arnold W., Financial Management: An Analytical Approach (Hamewood, Ill.: Richard D. Irwin, Inc., 1963), p. 73Google Scholar. Others interpret the profitability index to be the ratio of the present value of inflows to the present value of outlays. Johnson, Robert W., Financial Management, Second edition (Boston: Allyn & Bacon, Inc., 1962), p. 190.Google Scholar

6 In the model, we have assumed the divisibility of investment proposals. If a proposal is non-fractional, investment must be either zero or some absolute amount, and a dichotomy exists. Problems of this sort having “either-or” conditions may be solved by integer programming. See Dantzig, George B., “On the Significance of Solving Linear Programming Problems with Some Integer Variables,” Econometrica, XXVIII (January 1960), pp. 30–44Google Scholar; and Gomory, Ralph E., “Outline of an Algorithm for Integer Solutions to Linear Programs,” Bulletin of the American Mathematical Society, LXIV (September 1958), pp. 275–278.Google Scholar

For example, with investment proposal #1, we could impose the condition that; 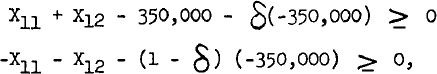where δ is an integer variable that must be 0 or 1. When δ = 0, X11 + X12 must be $350,000. When δ = 1, X11 + X12 must be zero. Consequently, we are assured that proposal #1 will not be fractional but will be either zero or $350,000.

While the direct problem is straightforward when integer-valued variables are involved, there may be complications in interpreting values for the dual variables. For exposition of the dual-variable problem in integer programming, see Gomory, Ralph E. and Baumol, William J., “Integer Programming and Pricing,” Econometrica, XXVIII (July 1960), pp. 521–550Google Scholar; and H. Martin Weingartner, 0p. cit., chapter 5.

7 Implicitly assumed is the fact that the quality of return on the investment proposals under consideration does not differ from the quality of return on existing investments.

8 To each direct problem there is a dual problem that makes use of the same data as are employed in the direct problem. The dual theorem of linear programming states that the optimal solution to the direct and the dual problem are the same. For explanation of the dual method, see Charnes, A. and Cooper, W. W., Management Models and Industrial Applications of Linear Programming, Vol. I (New York: John Wiley & Sons, Inc., 1961Google Scholar); Garvin, Walter W., Introduction to Linear Programming (New York: McGraw-Hill Book Company, Inc., 1960Google Scholar); Hadley, G., Linear Programming (Reading, Pa.: Addison-Wesley Publishing Company, Inc., 1962Google Scholar), or other texts dealing with linear programming.

9 Optimal use would involve investing an additional $0.30 in proposal #1, $0.15 in proposal #2, a $0.1+5 decrease in investment in proposal #6, an $0.80 increase in short-term borrowings, and an $0.80 decrease in long-term borrowings. The dual variable W18 = .0315 is valid only within certain limits. We can increase short-term debt and decrease long-term debt by only $80,000 before inequality (lq) and the non-negative requirement become binding. On the other hand, investment in proposal #6 can increase only $44,250 before inequality (lg) becomes binding. Consequently, W18* = .0315 remains valid for $151,666.67 ≤:(W.C. - Min. W.C.) ≤ $350,000.

10 Optimal employment of a $1 increase in the right-hand side of inequality (lu) would involve a $1.20 increase in proposal #1, a $0.60 increase in proposal #2, a $1.80 decrease in proposal #6, an $0.80 decrease in short-term borrowings, and an $0.80 increase in long-term borrowings. The value W20* = .126 remains valid for $325,416.67, ≤(W.C. – 14 L.T.D.) ≤$464,305.55. At $325,416.67, inequality (lg) becomes binding and precludes further investment in proposal #6, while at $464, 305.55, further reductions in investment proposal #6 would not be possible.

11 Optimal adjustment would involve increasing investment in proposal #1 by $180,500, to $350,000, an increase in investment proposal #2 of $129,460.53 to $184,210.53, elimination of investment of $200,000 in proposal #4, investment of $95,789.47 in proposal #5, elimination of investment of $205,750 in proposal #6, a decrease of $160,263.16 in shortterm borrowings, and an increase of a like amount in long-term borrowings.

12 Optimal employment would involve a $1.67 increase in proposal #1, a $7.50 decrease in proposal #2, and a $5.83 increase in proposal #6. As can be determined, W21* = .25833 remains valid for $2,300 ≤ Y - 2C ≤$32,300. Below $2,300, inequality (lc) becomes binding on further increases in proposal #2. Above $32,300, further decreases in proposal #2 are not possible.

13 We ignore the problem of deviations from desired dividends having an effect on the cost of capital by assuming that the moderate changes in dividends under consideration will not affect the cost of capital.

14 Optimal adjustment would involve increasing investment in proposal #1 by $12,166.67 to $181,666.67, elimination of the $54,750 investment in proposal #2, and increasing investment in proposal #6 by $42,583.33 to $248,333.33.