Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T10:50:42.310Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Uniqueness of Portfolio Choice

Published online by Cambridge University Press:  19 October 2009

Laurie Davies  and
Gerd Ronning
Get access Rights & Permissions [Opens in a new window]

Extract

In [1] the authors proved the following proposition.

Proposition 1: If the positive random variables 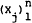are exchangeable and linearly independent and if u(x) is strictly concave and satisfies

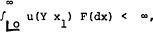
then the unique optimal choice is given by .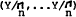

Type
Communications
Information
Journal of Financial and Quantitative Analysis , Volume 11 , Issue 3 , September 1976 , pp. 481 - 484
Copyright
Copyright © School of Business Administration, University of Washington 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Davies, P. L., and Ronning, G.. “Existence, Uniqueness and Continuity of Portfolio Choice.” Zeitschrift fur Nationalokonomie, vol. 34 (1974), pp. 137–143.CrossRefGoogle Scholar
[2]Feller, W.An Introduction to Probability Theory and Its Applications, vol. 2. New York: Wiley, 1966.Google Scholar
[3]Ramachandran, B., and Rao, C. R.. “Solutions of Functional Equations Arising in Some Regression Problems and a Characterization of the Cauchy Law.” Sankhya, Ser. A., vol. 32 (1970), pp. 1–30.Google Scholar
[4]Samuelson, P. A. “General Proof that Diversification Pays.” Journal of Financial and Quantitative Analysis, vol. 2 (1967), pp. 1–13.CrossRefGoogle Scholar
[5]Samuelson, P. A. “Limited Liability, Short Selling, Bounded Utility, and Infinite-Variance Stable Distributions.” Journal of Financial and Quantitative Analysis, September 1976.Google Scholar
[6]Shimizu, R. “Characteristic Functions Satisfying a Certain Functional Equation (1).” Ann. Inst. Statist. Math., vol. 20 (1968), pp. 187–209.CrossRefGoogle Scholar