Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-18T17:27:16.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Why Naive 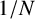$ 1/N $ Diversification Is Not So Naive, and How to Beat It?

Published online by Cambridge University Press:  16 October 2023

Ming Yuan  and
Guofu Zhou Open the ORCID record for Guofu Zhou [Opens in a new window]
Ming Yuan
Affiliation:
Department of Statistics, Columbia University ming.yuan@columbia.edu
Guofu Zhou*
Affiliation:
Olin School of Business, Washington University in St. Louis
*
zhou@wustl.edu (corresponding author)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show theoretically that the usual estimated investment strategies will not achieve the optimal Sharpe ratio when the dimensionality is high relative to sample size, and the 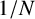$ 1/N $ rule is optimal in a 1-factor model with diversifiable risks as dimensionality increases, which explains why it is difficult to beat the 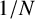$ 1/N $ rule in practice. We also explore conditions under which it can be beaten, and find that we can outperform it by combining it with the estimated rules when $ N $ is small, and by combining it with anomalies or machine learning portfolios, conditional on the profitability of the latter, when 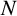$ N $ is large.

Type
Research Article
Information
Journal of Financial and Quantitative Analysis , First View , pp. 1 - 32
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of the Michael G. Foster School of Business, University of Washington

Footnotes

We are extremely grateful to two anonymous referees and Thierry Foucault (the editor) for their very detailed and insightful comments that have helped to improve the paper enormously. We are also grateful to Victor DeMiguel, John Dooley, Lorenzo Garlappi, Raymond Kan, Nathan Lassance, $ \overset{\smile }{\mathrm{L}} $uboš Pástor, Christopher Reilly, Landon Ross, Jun Tu, Raman Uppal, Xiaolu Wang, Alex Weissensteiner, Michael Wolf, Paolo Zaffaroni, Yingguang Zhang, Ge Zhe, and seminar and conference participants at Capital University of Economics and Business, Boston College, Fudan University, Louisiana State University, Peking University, University of Manitoba, University of Nottingham, Washington University in St. Louis, the 2021 International Conference on Computational and Financial Econometrics, and 2022 China International Conference for very helpful comments. Yuan was supported in part by the Columbia-CityU/HK collaborative project that is supported by the InnoHK Initiative, The Government of the HKSAR, and the AIFT Lab. We thank Songrun He for outstanding research assistance.

References

Ao, M.; Li, Y.; and Zhen, X.. “Approaching Mean-Variance Efficiency for Large Portfolios.” Review of Financial Studies, 32 (2019), 2890–2919.CrossRefGoogle Scholar
Avramov, D.; Cheng, S.; Metzker, L.; and Voigt, S.. “Machine Learning Versus Economic Restrictions: Evidence from Stock Return Predictability.” Management Science, 69 (2023), 2547–3155.CrossRefGoogle Scholar
Barillas, F.; Kan, R.; Robotti, C.; and Shanken, J.. “Model Comparison with Sharpe Ratios.” Journal of Financial and Quantitative Analysis, 55 (2020), 1840–1874.CrossRefGoogle Scholar
Basak, K.; Jagannathan, R.; and Ma, T.. “Jackknife Estimator for Tracking Error Variance of Optimal Portfolios.” Management Science, 55 (2009), 990–1002.CrossRefGoogle Scholar
Bawa, V.; Brown, S.; and Klein, R.. Estimation Risk and Optimal Portfolio Choice. Amsterdam, Netherlands: North-Holland (1979).Google Scholar
Berk, B., and van Binsbergen, J.. “Assessing Asset Pricing Models Using Revealed Preference.” Journal of Financial Economics, 119 (2016), 1–23.CrossRefGoogle Scholar
Bodnar, T.; Parolya, N.; and Schmid, W.. “Estimation of the Global Minimum Variance Portfolio in High Dimensions.” European Journal of Operational Research, 266 (2018), 371–390.CrossRefGoogle Scholar
Bodnar, T.; Okhrin, Y.; and Parolya, N.. “Optimal Shrinkage-Based Portfolio Selection in High Dimensions.” Journal of Business and Economic Statistics 41 (2023), 140–156.CrossRefGoogle Scholar
Brown, S. “Optimal Portfolio Choice Under Uncertainty: A Bayesian Approach.” Ph.D. dissertation, University of Chicago (1976).Google Scholar
Chen, L.; Pelger, M.; and Zhu, J.. “Deep Learning in Asset Pricing.” Management Science, forthcoming (2024).Google Scholar
Chen, J., and Yuan, M.. “Efficient Portfolio Pelection in a Large Market.” Journal of Financial Econometrics, 14 (2016), 496–524.CrossRefGoogle Scholar
Chen, A., and Zimmermann, T.. “Open Source Cross-Sectional Asset Pricing.” Critical Finance Review, forthcoming (2024).Google Scholar
Chincarini, L., and Kim, D.. Quantitative Equity Portfolio Management, 2nd ed. New York, NY: McGraw Hill (2023).Google Scholar
Chinco, A.; Clark-Joseph, A.; and Ye, M.. “Sparse Signals in the Cross-Section of Returns.” Journal of Finance, 74 (2019), 449–492.CrossRefGoogle Scholar
DeMiguel, V.; Garlappi, L.; and Uppal, R.. “Optimal Versus Naive Diversification: How Inefficient is the $ 1/N $ Portfolio Strategy?” Review of Financial Studies, 22 (2009), 1915–1953.CrossRefGoogle Scholar
DeMiguel, V.; Garlappi, L.; Nogales, F.; and Uppal, R.. “A Generalized Approach to Portfolio Optimization: Improving Performance by Constraining Portfolio Norms.” Management Science, 55 (2009), 798–812.CrossRefGoogle Scholar
DeMiguel, V.; Martín-Utrera, A.; and Nogales, F.. “Parameter Uncertainty in Multiperiod Portfolio Optimization with Transaction Costs.” Journal of Financial and Quantitative Analysis, 50 (2015), 1443–1471.CrossRefGoogle Scholar
DeMiguel, V.; Martín-Utrera, A.; Nogales, F.; and Uppal, R.. “A Transaction-Cost Perspective on the Multitude of Firm Characteristics.” Review of Financial Studies, 33 (2020), 2180–2222.CrossRefGoogle Scholar
Duchin, R., and Levy, H.. “Markowitz Versus the Talmudic Portfolio Diversification Strategies.” Journal of Portfolio Management, 35 (2009), 71–74.CrossRefGoogle Scholar
Fama, E., and French, K.. “Common Risk Factors in the Returns on Stocks and Bonds.” Journal of Financial Economics, 33 (1993), 3–56.CrossRefGoogle Scholar
Ferson, W., and Siegel, A.. “The Efficient Use of Conditioning Information in Portfolios.” Journal of Finance, 56 (2001), 967–982.CrossRefGoogle Scholar
Frahm, G., and Memmel, C.. “Dominating Estimators for Minimum-Variance Portfolios.” Journal of Econometrics, 159 (2010), 289–302.CrossRefGoogle Scholar
Freyberger, J.; Neuhierl, A.; and Weber, M.. “Dissecting Characteristics Nonparametrically.” Review of Financial Studies, 33 (2020), 2326–2377.CrossRefGoogle Scholar
Gu, S.; Kelly, B.; and Xiu, D.. “Empirical Asset Pricing via Machine Learning.” Review of Financial Studies, 33 (2020), 2223–2227.CrossRefGoogle Scholar
Grinold, R., and Kahn, R.. Active Portfolio Management: Quantitative Theory and Applications. New York, NY: McGraw Hill (1999).Google Scholar
Hafner, C., and Wang, L.. “Dynamic Portfolio Selection with Sector-Specific Regularization.” Econometrics and Statistics, forthcoming (2023).Google Scholar
Han, Y.; He, A.; Rapach, D.; and Zhou, G.. “Cross-Sectional Expected Returns: New Fama–MacBeth Regressions in the Era of Machine Learning.” Working Paper, Washington University in St. Louis (2023).Google Scholar
Harvey, C. R., and Liu, Y. “Lucky Factors.” Journal of Financial Economics, 141 (2021), 413–435.CrossRefGoogle Scholar
He, A., and Zhou, G.. “Diagnostics of Asset Pricing Models.” Financial Management, forthcoming (2024).Google Scholar
Huang, C., and Litzenberger, R.. Foundations for Financial Economics. Amsterdam, Netherlands: North-Holland (1988).Google Scholar
Hutchinson, J.; Lo, A.; and Poggio, T.. “A Nonparametric Approach to Pricing and Hedging Derivative Securities via Learning Networks.” Journal of Finance, 49 (1994), 851–889.CrossRefGoogle Scholar
Jaganathan, R., and Ma, T.. “Risk Reduction in Large Portfolios: Why Imposing the Wrong Constraints Helps.” Journal of Finance, 58 (2003), 1651–1683.CrossRefGoogle Scholar
Jorion, P. “Bayes-Stein Estimation for Portfolio Analysis.” Journal of Financial and Quantitative Analysis, 21 (1986), 279–292.CrossRefGoogle Scholar
Kan, R.; Wang, X.; and Zheng, X.. “In-Sample and Out-of-Sample Sharpe Ratios of Multi-Factor Asset Pricing Models.” Working Paper, University of Toronto (2020).CrossRefGoogle Scholar
Kan, R.; Wang, X.; and Zhou, G.. “Optimal Portfolio Choice with Estimation Risk: No Risk-Free Asset Case.” Management Science, 22 (2022), 2047–2068.CrossRefGoogle Scholar
Kan, R., and Zhou, G.. “Optimal Portfolio Choice with Parameter Uncertainty.” Journal of Financial and Quantitative Analysis, 42 (2007), 621–656.CrossRefGoogle Scholar
Kempf, A., and Memmel, C.. “Estimating the Global Minimum Variance Portfolio.” Schmalenbach Business Review, 58 (2006), 332–348.CrossRefGoogle Scholar
Kirby, C., and Ostdiek, B.. “It’s All in the Timing: Simple Active Portfolio Strategies that Outperform Naive Diversification.” Journal of Financial and Quantitative Analysis, 47 (2012), 437–467.CrossRefGoogle Scholar
Kozak, S.; Nagel, S.; and Santosh, S.. “Shrinking the Cross Section.” Journal of Financial Economics, 135 (2020), 271–292.CrossRefGoogle Scholar
Lassance, N. “Maximizing the Out-of-Sample Sharpe Ratio.” Working Paper, UCLouvain (2021).CrossRefGoogle Scholar
Lassance, N., and Martin-Utrera, A.. “Shrinking Against Sentiment: Exploiting Latent Asset Demand in Portfolio Selection.” Working Paper, UCLouvain (2022).Google Scholar
Lassance, N.; Martn-Utrera, A.; and Simaan, M.. “The Risk of Expected Utility Under Parameter Uncertainty.” Management Science, forthcoming (2024).CrossRefGoogle Scholar
Lassance, N.; Vanderveken, R.. and Vrins, F.. “On the Optimal Combination of Naive and Mean-Variance Portfolio Strategies.” Working Paper, UCLouvain (2022).CrossRefGoogle Scholar
Ledoit, O., and Wolf, M.. “Improved Estimation of the Covariance Matrix of Stock Returns with an Application to Portfolio Selection.” Journal of Empirical Finance, 10 (2003), 603–621.CrossRefGoogle Scholar
Ledoit, O., and Wolf, M.. “A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices.” Journal of Multivariate Analysis, 88 (2004), 365–411.CrossRefGoogle Scholar
Ledoit, O., and Wolf, M.. “Nonlinear Shrinkage of the Covariance Matrix for Portfolio Selection: Markowitz Meets Goldilocks.” Review of Financial Studies, 30 (2017), 4349–4388.CrossRefGoogle Scholar
MacKinlay, A., and Pástor, L̆.. “Asset Pricing Models: Implications for Expected Returns and Portfolio Selection.” Review of Financial Studies, 13 (2000), 883–916.CrossRefGoogle Scholar
Markowitz, H. “Portfolio Selection.” Journal of Finance, 7 (1952), 77–91.Google Scholar
McLean, R., and Pontiff, J.. “Does Academic Research Destroy Return Predictability?” Journal of Finance, 71 (2016), 5–32.CrossRefGoogle Scholar
Meucci, A. Risk and Asset Allocation. New York, NY: Springer (2005).CrossRefGoogle Scholar
Pflug, G.; Pichler, A.; and Wozabal, D.. “The $ 1/N $ Investment Strategy is Optimal Under High Model Ambiguity.” Journal of Banking and Finance, 36 (2012), 410–417.CrossRefGoogle Scholar
Rapach, D.; Strauss, J.; and Zhou, G.. “International Stock Return Predictability: What Is the Role of the United States?” Journal of Finance, 68 (2013), 1633–1662.CrossRefGoogle Scholar
Raponi, V.; Robotti, C.; and Zaffaroni, P.. “Testing Beta-Pricing Models Using Large Cross-Sections.” Review of Financial Studies, 33 (2020), 2796–2842.CrossRefGoogle Scholar
Raponi, V.; Uppal, R.; and Zaffaroni, P.. “Robust Portfolio Choice.” Working Paper, Imperial College (2021).CrossRefGoogle Scholar
Ross, S. “The Arbitrage Theory of Capital Asset Pricing.” Journal of Economic Theory, 13 (1976), 341–360.CrossRefGoogle Scholar
Shi, F.; Shu, L.; Yang, A.; and He, F.. “Improving Minimum-Variance Portfolios by Alleviating Overdispersion of Eigenvalues.” Journal of Financial and Quantitative Analysis, 55 (2020), 2700–2731.CrossRefGoogle Scholar
Tu, J., and Zhou, G.. “Markowitz Meets Talmud: A Combination of Sophisticated and Naive Diversification Strategies.” Journal of Financial Economics, 99 (2011), 204–215.CrossRefGoogle Scholar
Yan, C., and Zhang, H.. “Mean-Variance Versus Naïve Diversification: The Role of Mispricing.” Journal of International Financial Markets, Institutions and Money, 48 (2017), 61–81.CrossRefGoogle Scholar